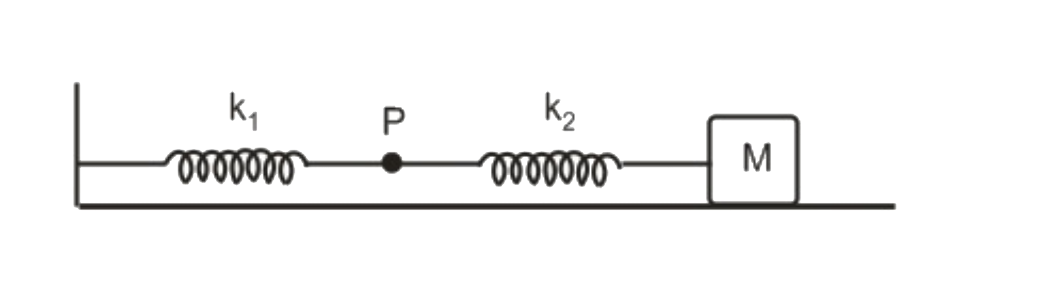
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is

$\frac{k_{1} A}{k_{2}}$

$\frac{k_{2} A}{k_{1}}$

$\frac{k_{1} A}{k_{1} + k_{2}}$

$\frac{k_{2} A}{k_{1} + k_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The mass $M$ shown in the figure oscillates in simple harmnonic motion and amplitude $A$ . The amplitude of the point $P$ is

A $\frac{k_{1} A}{k_{2}}$
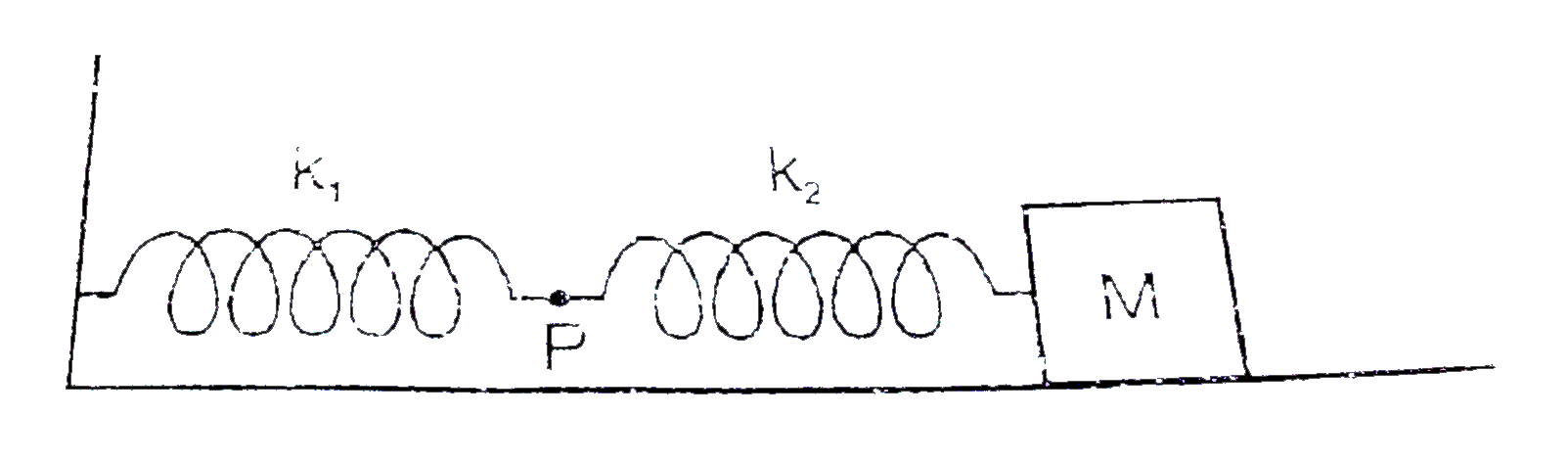B $\frac{k_{2} A}{k_{1}}$
C $\frac{k_{1} A}{k_{1} + k_{2}}$
D $\frac{k_{2} A}{k_{1} + k_{2}}$
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is $V_{0}$ . Assume springs are massless. Select the correct option/s

AAmplitude of potential energy is springs $S_{1}$ and $S_{2}$ is respectivley $\frac{1}{9} k A^{2}$ and $k A^{2}$
BAmplitude of potential energy is $S_{1}$ and $S_{2}$ is respectively $\frac{2}{9} k A^{2}$ and $\frac{1}{9} k A^{2}$
C $V_{0} = A \sqrt{\frac{8 k}{27 M}}$
D $V_{0} = A \sqrt{\frac{8 k}{81 M}}$
A simple harmonic motino has amplitude A and time period T. The maxmum velocity will be
A $4 A T$
B $\frac{2 A}{T}$
C $2 π \sqrt{\frac{A}{T}}$
D $\frac{2 π A}{T}$