Complete Solutions to NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION) of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| MTG GUIDE | NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
The universal law of gravitational is the force law known also as the
View SolutionTwo identical spheres of radius R made of the same material are kept at a distance d apart. Then the gravitational attraction between them is proportional to
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle PQR and a mass of 2 kg is placed at the centroid O of the triangle which is at a distance of `sqrt(2)m` from each of the vertices of the triangle. The force, in newton, acting on the mass of 2 kg is :
View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
View SolutionMass `M` is split into two parts `m` and `(M-m)`, which are then separated by a certain distance. What is the ratio of `(m//M)` which maximises the gravitational force between the parts ?
View SolutionThree indentical bodes of mass M are locatd at the verticles of an equailateral triangle of side L they revolve undr the effect of mutual gravitational force in a circular orbit circumscibing the traingle while preserving the equilateral triangle their orbital velocity is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of `d = sqrt(3)R` from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionTwo solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionIf two particles each of mass `m` are placed at the two vertices of an equilateral triangle of side `a`, then the resultant gravitational force on mass `m` placed at the third vertex is
View SolutionA point mass m is placed inside a spherical shell of radius R and mass M at a distance `R/2` form the centre of the shell. The gravitational force exerted by the shell on the point mass is
View SolutionThe magnitudes of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `E_(1)` and `E_(2)` respectively. Then:
View SolutionTwo point masses A and B having masses in the ratio `4:3` are separated by a distance of 1m. When another point mass C of mass M is placed in between A and B, the force between A and C is `(1/3)^(rd)` of the force between B and C. Then the distance C from A is
View SolutionA planet of radius `R=(1)/(10)xx(radius of Earth)` has the same mass density as Earth. Scientists dig a well of depth`(R )/(5)` on it and lower a wire of the same length and a linear mass density `10^(-3) kg m(_1)` into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth`=6xx10^6m` and the acceleration due to gravity on Earth is `10ms^(-2)`
View SolutionThe gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
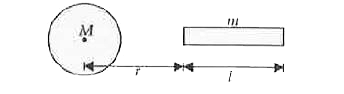
View Solution
NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION) questions and complete solutions for chapter GRAVITATION of MTG GUIDE PHYSICS (HINGLISH) of Class 11
All Exercises from MTG GUIDE Class 11 PHYSICS GRAVITATION
- AIPMT/NEET MCQS
- CHECK YOUR NEET VITALS
- ILLUSTRATION
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION)