Mass M is split into two parts m and (M−m), which are then separated by a certain distance. What is the ratio of (m/M) which maximises the gravitational force between the parts ?
1:4
1:3
1:2
1:1
The correct Answer is:C
If r is the distance between m and (M-m), the gravitational force will be
F=Gm(M−m)r2=Gr2(mM−m2)
For F to be maxim dFdm=0 (as M and rare constants)
∴ddm[Gr2(mM−m2)]=0 or M−2m=0 or mM=12(AsGr2≠0)
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
A mass M is split into two parts m and (M-m) which are then separated by certain distance. Find ratio (m/M) to maximise the gravitational force F=Gm(M−m)r2 between the parts.
Here G = gravitational constant and r is the distance between m and (M-m).
View SolutionMass M is divided into two parts m1, and m2, For a given separation the ratio of m1M for which the gravitational attraction between the two parts becomes maximum is
View Solution
Knowledge Check
A mass M splits into two parts m and (M - m) , which are then separated by a certain distance. Wha ratio (m/M) maximize the gravitational force between the path ?
A23B34C12D13A mass M splits into two parts m and (M-m), which are separated by a cetain distance. The ratio m/M which maximizes the gravitational force between the parts is
A1:4B1:3C1:2D1:1A mass M at rest is broken into two pieces having masses m and (M-m). The two masses are then separated by a distance r. The gravitational force between them will be maximum when the ratio of the masses [m : (M-m) of the two parts is
A1:1B1:2C1:3D1:4
A body of mass (2M) splits into four masses {m,M−m,m,M−m}, which are rearranged to form a square as shown in the figure. The ratio of Mm for which, the gravitational potential energy of the system becomes maximum is x : 1 . The value of x is ________.
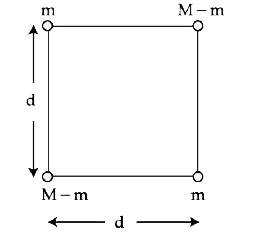
View SolutionTwo spheres of masses (m) and (M - m) are prepared from a sphere of mass M. They are kept at a distance x. For what ratio of mM will the gravitational attraction between them be maximum ?
View SolutionTwo point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero, is :-
View Solution
