Question

A planet of radius $R=\frac{1}{10}\times \left(radiusofEarth\right)$ has the same mass density as Earth. Scientists dig a well of depth$\frac{R}{5}$ on it and lower a wire of the same length and a linear mass density ${10}^{-3}kgm(\_1)$ into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth$=6\times {10}^{6}m$ and the acceleration due to gravity on Earth is $10m{s}^{-2}$

Options

A. 96N
B. 108N
C. 120N
D. 150N

Answer

B

Explanation

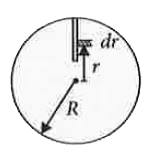
Gravitational field inside the planet at a distance r from centre,
`g_i = (GM)/(R^3) r = (G (4/3 pi R^3) rho )/(R^3) r = 4/3 G pi r rho`
Force applied by the person on the wire at rest is the weight of the wire. Since, gravitational field is variable so force on each part of the wire is different. Consider a small portion dr of the wire at a distance r from centre of the planet, so its weight will be
`dW = (dm)g_i = (lamda dr) (4/3 G pi r rho) = (4/3 Gpi rho) (lamda r dr)`
Net weight , `W =int dW = (4/3 G pi rho lamda) int_((4R)/(5))^(R ) rdr`
`W= (4/3 G pi rho lamda) (9/50) R^2`
Density of the earth , ` rho (M_E)/(4/3 pi R_E^3) ,` also , ` R = (R_E)/(10)`
Putting the values of `rho` and R in equation (i) , we get
` W = ((9)/(5 xx 10^3)) g_E lamda R_E = (9)/(5 xx 10^3) xx 10 xx 10^(-3) xx 6 xx 10^6 = 108N`
so , net force applied by the person to hold the wire = 108N