Complete Solutions to NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY) of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| MTG GUIDE | NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY) |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
The escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of `45^@` with the vertical, the escape velocity will be
View SolutionA ball is thrown vertically upwards with a velocity equal to half the escape velocity from the surface of the earth. The ball rises to a height h above the surface of the earth. If the radius of the earth is R, then the ratio `h/R` is
View SolutionA body is projected up with a velocity equal to `3//4th` of the escape velocity from the surface of the earth. The height it reaches is (Radius of the earth is `R`)
View SolutionThe escape velocity corresponding to a planet of mass `M` and radius `R` is `50 km s^(-1)`. If the planet's mass and radius were `4M` and `R`, respectively, then the corresponding escape velocity would be
View SolutionThe moon has a mass of `(1)/(81)` that of the earth and radius of `(1)/(4)` that of the earth. The escape speed from the surface of the earth is 11.2 km`//`s. The escape speed from surface of the moon is-
View SolutionThe escape velocity of an object from the earth depends upon the mass of the earth ( M ), its mean density `(rho)`, its radius ( R ) and the gravitational constant ( G ). Thus the formula for escape velocity is
View SolutionA particles is fired vertically from the surface of the earth with a velocity `Kv_(e)` , where `u_(e)` is the escape velcocity ans `Klt 1`. Neglecting air resistance , calcualte the heightto which it will rise from the surface of the earth .(R= radius of the earth ).
View SolutionThe escape velocity form the earth is 11 `kms^(-1)` the esacpe velocity from a planet having twice the radius and the same mean denisty as the earth would be
View SolutionThe escape velocity of a particle of mass `m` varies as
View SolutionWhat is the escape velocity for body on the surface of planet on which the accelearation due to gravity is `(3.1)^(2)ms^(2)` and whose radius is 8100 km ?
View SolutionThere are two planets. The ratio of radius of two planets is `k` but ratio of acceleration due to gravity of both planets is g. What will be the ratio of their escape velocity ?
View SolutionTwo stars each of mass `M` and radius `R` are approaching each other for a head-on collision. They start approaching each other when their separation is `rgt gtR`. If their speed at this separation are negligible, the speed `v` with which they collide would be
View SolutionA planet in a distant solar systyem is 10 times more massive than the earth and its radius is 10 times smaller. Given that the escape velocity from the earth is `11kms^(-1)`, the escape velocity from the surface of the planet would be
View SolutionTwo balls A and B are thrown vertically upwards from the same location on the surface of the earth with velocities `2 sqrt((gR)/(3)) ` and `sqrt((2gR)/(3))` respectively, where R is the radius of the earth and g is the acceleration due to gravity on the surface of the earth. The ratio of the maximum height attained by A to that attained by B is
View SolutionThe radius in kilometers, to which the present radius of the earth (R = 6400 km) is to be compressed so that the escape velocity velocity is increased ten times is
View SolutionEscape velocity of a body from the surface of earth is 11.2km/sec. from the earth surface. If the mass of earth becomes double of its present mass and radius becomes half of its present radius then escape velocity will become
View SolutionA particle of mass ‘m’ is kept at rest at a height 3R from the surface of earth, where ‘R’ is radius of earth and ‘M’ is mass of earth. The minimum speed with which it should be projected, so that it does not return back, is (g is acceleration due to gravity on the surface of earth)
View SolutionA body is released from a point of distance `R'` from the centre of earth. Its velocity at the time of striking the earth will be `(R’gtR_(e))`
View SolutionTwo spherical planets P and Q have the same uniform density `rho,` masses `M_p and M_Q` and surface areas A and 4A respectively. A spherical planet R also has uniform density `rho` and its mass is `(M_P + M_Q).` The escape velocities from the plantes P,Q and R are `V_P V_Q and V_R` respectively. Then
View SolutionIf the escape velocity of a planet is 3 times that of the earth and its radius is 4 times that of the earth, then the mass of the planet is (Mass of the earth = `6 xx 10^24 kg`)
View SolutionThe escape velocity of a body from the surface of earth is
View SolutionTwo satellites `M` and `N` go around the earth in circular orbits at heights of `R_(M)` and `R_(N)` respectively from the surrface of the earth. Assuming the earth to be a uniform sphere of radius `R_(E)`, the ratio of velocities of the satellites `(V_(M))/(V_(N))` is
View SolutionAssuming density d of a planet to be uniform, we can say that the time period of its artificial satellite is proportional to
View SolutionTwo satellite of mass `m` and `9 m` are orbiting a planet in orbits of radius `R`. Their periods of revolution will be in the ratio of
View SolutionAn artificial satellite moving in circular orbit around the earth has total (kinetic + potential) energy `E_(0)`. Its potential energy and kinetic energy respectively are :
View SolutionThe time period of an earth satellite in circular orbit is independent of
View SolutionA satellite is launched into a circular orbit of radius 'R' around earth while a second satellite is launched into an orbit or radius 1.02 R. The percentage difference in the time periods of the two satellites is
View SolutionThe ratio of the energy required to raise a satellite upto a height h above the surface of earth to that the kinetic energy of the satellite into the orbit there is (R=radius of earth)
View SolutionIn a satellite if the time of revolution is `T`, then kinetic energy is proportional to
View SolutionTwo identical satellites A and B revolve round the earth in circular orbits at distance R and 3R from the surface of the earth. The ratio of the linear momenta of A and B is (R = radius of the earth)
View SolutionAn earth satellite is moving round the earth in a circular orbit . For such a satellite which of the following statement is wrong ?
View SolutionAn asteroid of mass `2 xx 10^(-4) M_e`, where `M_e` is the mass of the earth, revolves in a circular orbit around the sun at a distance that is twice earth's distance from the sun. Find the ratio of the kinetic energy of the asteroid to that of earth
View SolutionTwo satellites are revolving around the earth in circular orbits of same radii. Mass of one satellite is `100` times that of the other. Then their periods of revolutions are in the ratio
View SolutionThe orbit of geostationary satellite is circular, the time period of satellite depeds on (i) mass of the satellite, (ii) mass of earth, (iii) readius of the orbit and (iv) height of the satellite from the surface of the earth
View SolutionThe distance of two satellites from the surface of the earth `R` and `7R`. There time periods of rotation are in the ratio
View SolutionThe escape velocity for a planet is `v_e`. A particle is projected from its surface with a speed `v`. For this particle to move as a satellite around the planet.
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height `2R` from the surface of the earth (`R`=radius of earth)
View SolutionA satellite is in a circular orbit very close to the surface of a planet. At some point it is given an impulse along its direction of motion, causing its velocity to increase `n` times . It now goes into an elliptical orbit. The maximum possible value of `n` for this to occur is
View SolutionAn artificial satellite is orbiting at a height of 1800 km from the earth's surface. The earth's radius is 6300 km and `g=10m/s^(2)` on its surface. What is the radial acceleration of the satellite?
View SolutionHow long will a satellite, placed in a circular orbit of radius that is `(1/4)^(th)` the radius of a geostationary satellite, take to complete one revolution around the earth?
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth. The height of the satellite above the surface of the earth is x R. Find the value of x.
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View SolutionThe kinetic energy of a satellite is 2 MJ. What is the total energy of the satellite?
View SolutionFigure shows the variation of energy with the orbit radius r of a satellite in a circular motion. Mark the correct statement.
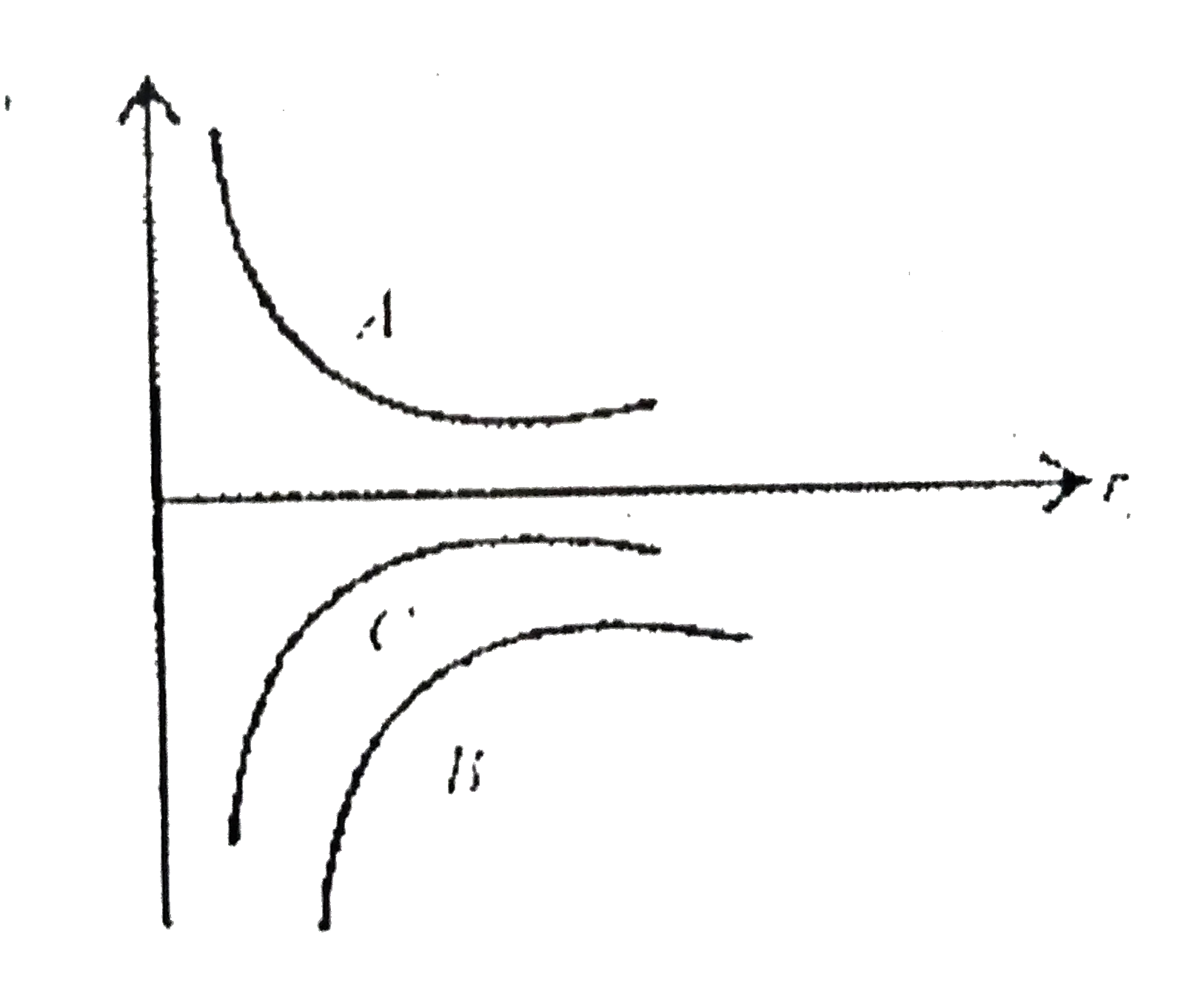
View SolutionA satellite is launched into a circular orbit of radius R around the earth. A second satellite is launched into an orbit of radius 4R. The ratio of their respective periods is
View SolutionThe total energy of a circularly orbiting satellite is
View SolutionEnergy required in moving a body of mass `m` from a distance 2R to 3R from centre of earth of mass M is
View SolutionIf r is the distance between the Earth and the Sun. Then, angular momentum of the Earth around the sun is proportional to
View SolutionThe time period `T` of the moon of planet mars (mass `M_(m)`) is related to its orbital radius `R` as (`G`=gravitational constant)
View SolutionHeight of geostationary satellite is
View Solution
NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY) questions and complete solutions for chapter GRAVITATION of MTG GUIDE PHYSICS (HINGLISH) of Class 11
All Exercises from MTG GUIDE Class 11 PHYSICS GRAVITATION
- AIPMT/NEET MCQS
- CHECK YOUR NEET VITALS
- ILLUSTRATION
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
- NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION)