The ratio of the energy required to raise a satellite upto a height h above the surface of earth to that the kinetic energy of the satellite into the orbit there is (R=radius of earth)

A

$R : h$

B

$h : R$

C

$R : 2 h$

D

$2 h : R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Energy required to raise the satellite to a height h from the surface of earth is
$U = - \frac{G M m}{(R + h)} - (- \frac{G M m}{R}) = \frac{G M m h}{R (R + h)}$
Kinetic energy of satellite is
$K = \frac{1}{2} m v_{0}^{2} = \frac{1}{2} m \frac{G M}{(R + h)} ∴ \frac{U}{K} = \frac{2 h}{R}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The ratio of energy required to raise a satellite to a height $h$ above the earth surface to that required to put it into the orbit is
A $h : 2 R$
B $2 h : R$
C $R : h$
D $h : R$
Question 2 - Select One
A geostationary satellite is at a height $h$ above the surface of earth. If earth radius is $R$ -

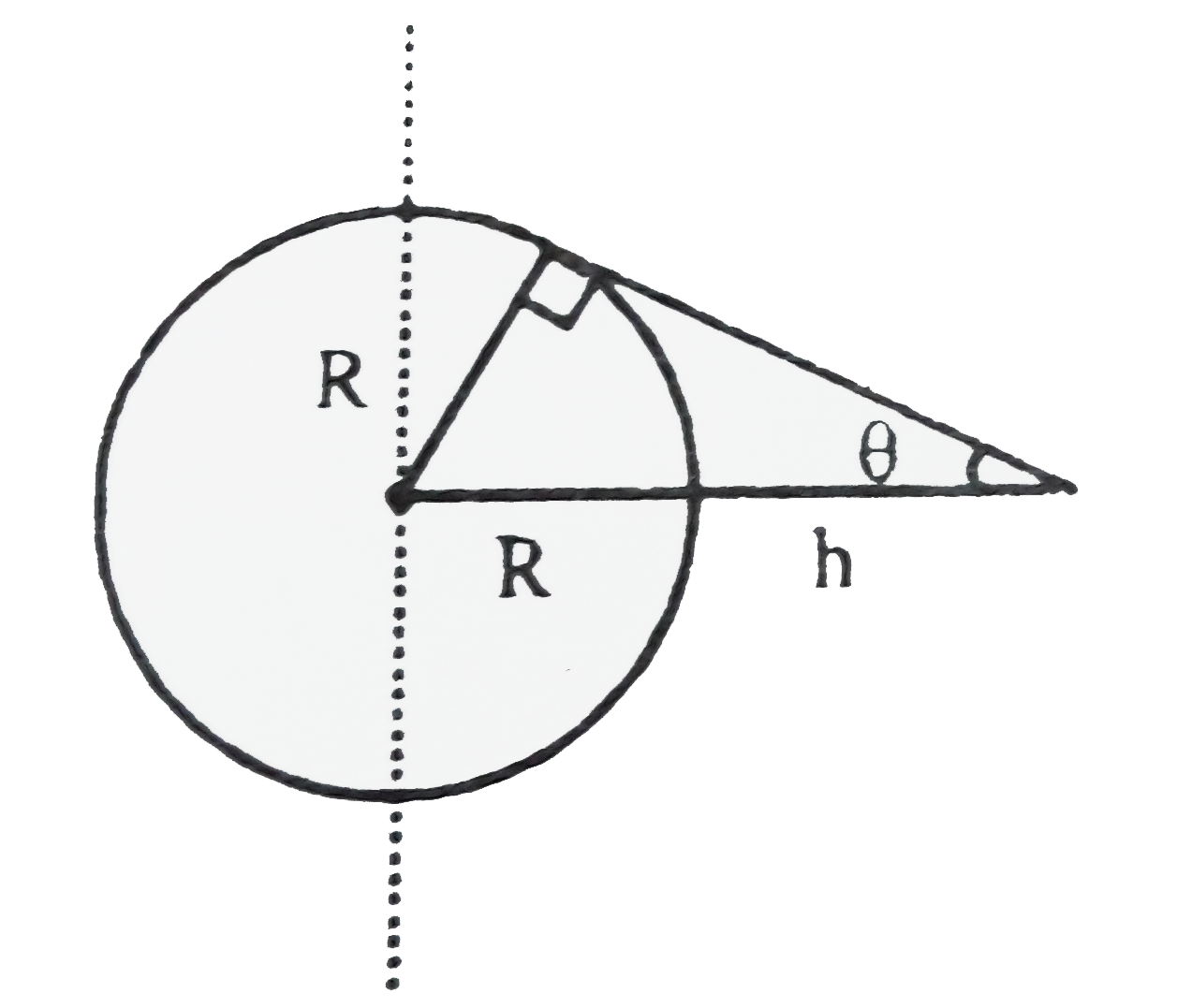AThe minimum colatitude on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
BThe maximum colatitudes on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
CThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + sin θ))$
DThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + cos θ)$
Question 3 - Select One
Let E be the energy required to raise a satellite to height $h$ above earth's surface and E' be the energy required to put the same satellite into orbit at that height. Then $E / E'$ is equal to
A $\frac{2 h}{(R + 2 h)}$
B $\frac{2 h}{(2 R + 3 h)}$
C $\frac{R}{R + h}$
D $\frac{2 R}{2 h + R}$

MTG GUIDE-GRAVITATION-NEET CAFE TOPICWISE PRACTICE QUESTIONS (ESCAPE VELOCITY)

Home
Ask Doubt
Profile