Complete Solutions to SOLVED EXAMPLE of chapter THERMAL PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMAL PROPERTIES OF MATTER |
| MODERN PUBLICATION | SOLVED EXAMPLE |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
A faulty thermometer reads `5^@C` and `99^@C` in ice and steam, respectively. If this thermometer reads `62^@C` , find the correct temperature in `""^@C` .
View SolutionA thermometer with wrong calibration reads melting point of ice as-`8^@C` and `50^@C` in place of `40^@C` . Calculate the boiling point of water on this scale.
View SolutionA thermometer is taken from the melting ice into a warm liquid which results in rise in mercury level to 1/5th of the distance between the lower and the upper fixed points. Calculate the temperature of liquid in kelvins.
View SolutionCalculate the temperature at which the reading on Fahrenheit scale is equal to half the reading of Celsius scale.
View SolutionA faulty constant volume thermometer using helium gas records a pressure of `1.65 xx 10^4` Pa at normal freezing point of water, and a pressure of `2.10 xx 10^4` Pa at normal boiling point of water. Using these observations, determine the temperature of absolute zero on the Celsius scale.
View SolutionFor what increase in temperature of a bras rod ,its length will increase by 0.5%
`alpha_("brass") = 0.00002^@C^(-1)`
View SolutionGaps are left while laying the railway lines in order to allow for expansion. The gap between steel rails of length 65 m is 3.56 cm at `15^@C` . Calculate the temperature at which the rails will just touch each other. Take, `O_("steel") = 1.1 xx 10^(-5)@C^(-1)`
View SolutionA blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the rim and the ring are `5.243 m` and `5.231 m` respectively at `27^(@)C`. To what temperature should the ring be heated so as to fit the rim of the wheel ? Coefficient of linear expansion of iron =` 1.20 xx 10^(-5) K^(-1)`
View SolutionThe length of a brass rod at `20^@C` is observed to be 0.8 m when measured by an iron scale, correct at `0^@C` . What will be the correct length of the rod at`0^@C` ? Take, `alpha_("iron") = 1.2 xx 10^(-5) ""^@C^(-1)`
`alpha_("brass") = 1.9 xx 10^(-5) ""^@C^(-1)`
View SolutionA clock with a brass pendulum keeps correct time at `30^@C` . How many seconds will it loose or gain if the temperature falls by `10^@C` ? Take, `alpha_("brass") = 0.000019^@C^(-1)`
View SolutionA metallic ball of radius 0.2 m is heated from 320 K to 522 K. What will be the increase in surface area of the ball? Given, coefficient of superficial expansion of the ball `= 3.4 xx 10^(-5)K^(-1)`
View SolutionWhen a glass block of volume `15,000 cm^3` is heated from `20^@C` to `40^@C` , its volume increases by `5 cm^3` . What is the coefficient of linear expansion of glass?
View SolutionA gasoline tank made of steel is filled completely with 60 litres of gasoline, both at a temperature of `12^@C` . How much gasoline will overflow when the temperature is increased to `25^@C` ?
`alpha_("steel") = 1.1 xx 10^(-5) ""^@C^(-1)`
`gamma_("gasoline") = 9.5 xx 10^(-4) ""^@C^(-1)`
View SolutionA geyser heats 5kg/min water , from `25^@C " to " 80^@C` . Find the rate of consumption of the fuel if the geyser operates on a gas burner , Take Heat of cosumbustion ` = 5 xx 10^4 J//g`
sepcific heat of water ` = 4.20 xx 10^3 J//kg//K`
View SolutionA sphere of aluminium of 0.047 kg is placed for sufficient time in a vessel containing boiling water, so that the sphere is at `100^(@)` C. It is then immediately transferred to 0.14 kg copper calorimeter containing 0.25 kg of water at `20^(@)` C. The temperature of water rises and attains a steady state at `23^(@)`Calculate the specific heat capacity of aluminium. (Give specific heat of copper `=0.386xx10^(3)Jkg^(-1)K^(-1))`.
View SolutionA thermally isolated vessel is maintained inside at `0^@C` and contains 200 g of water. When the air above the water is pumped out, some of the water freezes while rest of it evaporated at `0^@C` itself. Determine the mass of water that freezed. Take, Latent heat of vapourisation of water at `0^@C = 2.19 xx 10^3 J//g`
Latent heat of fusion of ice =` 3.36 xx 10^2 J//g`
View SolutionIn a container containing 0.2 kg of water at `40^@C` , 0.2 kg of ice at `0^@C` is mixed. Calculate the heat of fusion of ice if the resulting temperature is `5.5^@C` . Take, Specific heat of water = `4186 J kg^(-1)K^(-1)`
View SolutionCalculate the heat required to convert 3 kg of ice at `-12^(@)C` kept in a calorimeter to steam at `100^(@)C` at atmospheric pressure. Given,
specific heat capacity of ice = `2100 J kg^(-1) K^(-1)`
specific heat capicity of water = `4186 J kg^(-1)K^(-1)`
Latent heat of fusion of ice = ` 3.35 xx 10^(5) J kg^(-1)`
and latent heat of steam = ` 2.256 xx 10^(6) J kg^(-1)` .
View SolutionFor a glass window of area `1500 cm^2` and thickness 0.5 cm, determine the rate of loss of heat if the temperature inside the window is `35^@C` and outside is `-2^@C` . Take, coefficient of thermal conductivity of glass `= 2.2 xx 10^(-3) cal s^(-1) cm^(-1) K^(-1)`
View SolutionWhen steam at `100^@C` is passed into a metal cylinder, water at `100 ^@C` is collected at the rate of 200 g/min. If the area and thickness of cylinder are `300 cm^2` and 20 mm, respectively, determine the temperature of the outer surface. Take, thermal conductivity of metal `= 0.424 cal s^(-1)`cm. Latent heat of steam `= 540 cal g^(-1)`
View SolutionOne end of 0.5 m long metal rod is in steam at `100^@C` and the other end is put in ice at `0^@C`. If ice melts at the rate of 10 g/min, calculate the thermal conductivity of the metal. Take, cross sectional area of `rod = 2pi cm^2` . Latent ice of heat = 80 cal/g
View SolutionOn the Dal lake of Kashmir, a layer of 2 cm thick ice is formed when the outside temperature is `-10^@C` . How much time it will take for the increase in thickness of ice by 0.5 mm? Take, Density of ice `= 1 g//c^3` m
Latent heat of ice = 80 cal/g
Thermal conductivity of ice = `0.008 cal s^(-1) cm^(-1) ""^@C^(-1)`
View SolutionA rectangular steel tank of thickness 2.5 cm is used to boil water by a constant temperature furnace. If the level of water inside the tank falls at a steady rate of 0.25 cm in 2 minutes due to vaporisation, find the temperature of the furnace.
Take, conductivity of steel `= 0.2 cal s^(-1) m^(-1) ""^@C^(-1)`
Latent heat of steam = 540 cal/g
View SolutionThree rods of equal length and equal area of cross section are connected end to end in series. The open end of the first rod (from left) is at a temperature of `300^@C` and that of the last rod is at `20^@C` in steady state. If the thermal conductivities of rods from left to right are in the ratio of 1: 3: 4, then find the temperatures of both the junctions.
View SolutionA 2m iron rod of uniform cross section has its one end in contact with ice at `0^@C` and the other end with water at `100^@C` . Find a point along the length of the rod at which a temperature of `150^@C` is maintained so that mass of ice melted is equal to mass of steam produced in the same time. Consider that the system is thermally isolated from the surroundings. Take, Latent heat of ice = 80 cal/g
Latent heat of vapourisation of water = 540 cal/g

View SolutionWhat is the temperature of steel-copper junction in the steady state of the system shown in fig. Length of the steel rod = 30.0 cm, length of the copper rod = 20.0 cm, temperature of the furnace = `300^(@)C`, temperature of cold end `=0^(@)C` . The area of cross-section of the steel rod is twice that of the copper rod. thermal conductivity of steel = `50 .2 Js^(-1) m^(-1) .^(@)C^(-1)` and of copper = `358 Js^(-1) m^(-1) .^(@)C^(-1)`.
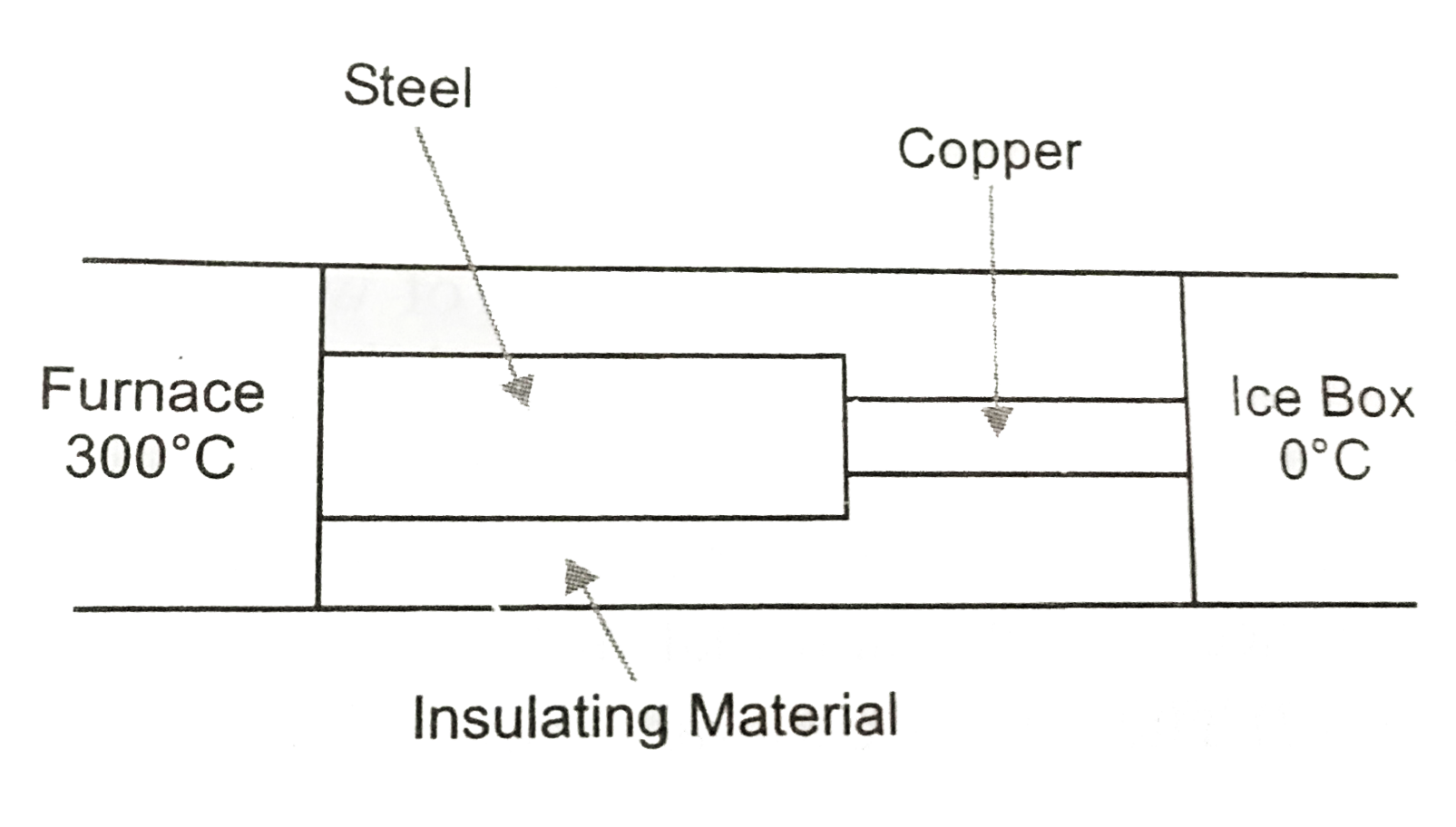
View SolutionAn iron bar (`L_(1) = 0.1 m, A_(1) = 0.02 m^(2) , K_(1) = 79 Wm^(-1) K^(-1)`) and a brass bar `(L_(2)=0.1 m , A_(2) = 0.02 m^(2), K_(2) = 109 Wm^(-1)K^(-1)`) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
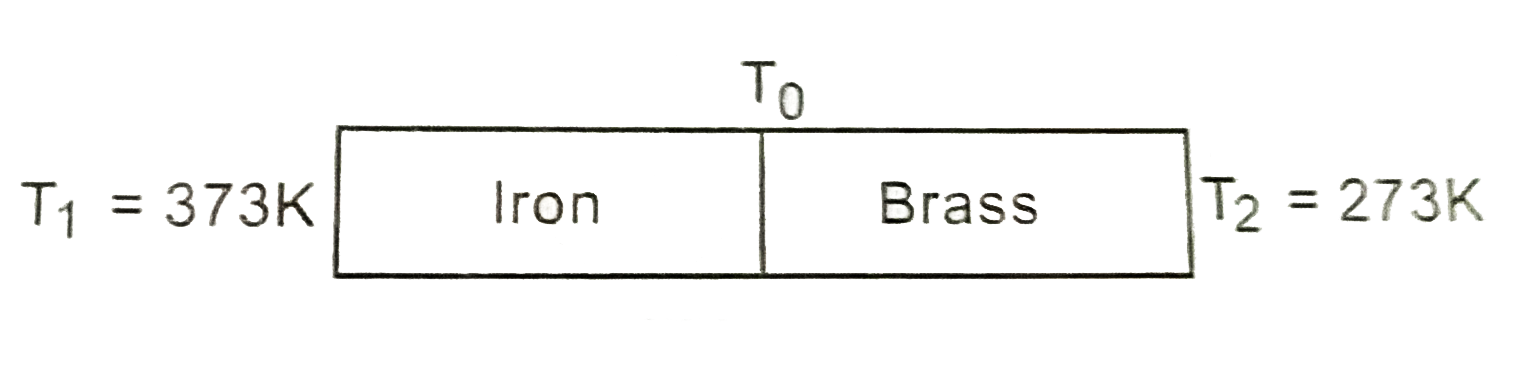 .
.
View SolutionA hot body at `70^@C` cools to `25^@` C in 15 min . Find its temperature after the next 10 mins. The temperature of the surroundings is `10^@C` .
View SolutionAt what temperature, a perfect black body will radiate energy at the rate of `6.48 W//cm^2` . Take, `sigma = 5.67 xx 10^(-8) Wm^(-2)`K^(-4)`
View SolutionDue to voltage fluctuations, the temperature of an electric bulbs rises from 2000 K to 3000 K. Calculate the percentage rise in the electric power consumed.
View SolutionCalculate the energy radiation by the sun in 2 mins if it is considered to be perfect sphere of radius `6.8 xx 10^8 m` and its surface temperature is approximately 6200 K. Take `sigma = 5.67 xx 10^(-8) Jm^(-2) s^(-1) K^(-4)`
View SolutionA thin brass rectangular sheet of sides 15.0 cm and 10.0 cm is heated in a furnace to `500^@C` and then taken out. Calculate the electric power that is needed to maintain the sheet at this temperature, given that the emissivity is 0.250. (Stefan-Boltzmann constant, `sigma = 5.67 xx 10^(-8) Wm^(-2) K^(-4)` )
View SolutionA sphere of radius 15 cm is at a temperature of `215^@C` . Find the maximum amount of heat which may be lost per second by radiation when the sphere is placed in an enclosure at `25^@C`. Take, `sigma = 5.67 xx 10^(-8) Wm^(-2) K^4`
View SolutionCompare the rate of loss of heat by one degree from a cup of hot coffee when it is at `100^@C` and at `40^@C` , in a room at `10^@C` . Consider the coffee to act as a black body.
View SolutionA hot body has a surface temperature of `1345^@C` . Calculate the wavelength at which it radiates maximum energy . Take .
Wein,s constant = 0.2898 cm K
View SolutionThe sun radiates maximum energy at a wavelength of 4753 Å. If the temperature of the sun is 6076 K, determine the temperature of a star for which maximum energy is emitted at 9300 Å
View SolutionA heated filament of a bulb is radiating maximum energy at wavelength `3.14 xx 10^(-5) ` cm. Determine the total amount of energy lost per second per unit area by the filament if the temperature of the surrounding air is `20^@C` . Take,
`b = 0.288 cm K`
`sigma = 5.77 xx 10^(-5) erg s^(-1) cm^(-2) K^(-4)`
View Solution
SOLVED EXAMPLE questions and complete solutions for chapter THERMAL PROPERTIES OF MATTER of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS THERMAL PROPERTIES OF MATTER
- CHAPTER PRACTICE TEST
- COMPETITION FILE (ASSERTION REASON TYPE QUESTION )
- COMPETITION FILE (EXEMPLAR PROBLEM OBJECTIVE TYPE QUESTION (MULTIPLE CHOICE QUESTION TYPE - I )
- COMPETITION FILE (EXEMPLAR PROBLEM OBJECTIVE TYPE QUESTION (MULTIPLE CHOICE QUESTION TYPE - II )
- COMPETITION FILE (EXEMPLAR PROBLEM SUBJECTIVE QUESTION (SHORT ANSWER TYPE QUESTION)
- COMPETITION FILE (EXEMPLAR PROBLEM SUBJECTIVE QUESTION (VERY SHORT ANSWER TYPE QUESTION)
- COMPETITION FILE (INTEGER TYPE QUESTION )
- COMPETITION FILE (MATRIX MATCH TYPE QUESTION )
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((A) MULTIPLE CHOICE QUESTION WITH ONLY ONE CORRECT ANSWER))
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) AIMPMT/NEET AND OTHER STATE BOARDS FOR MEDICAL ENTRANCE)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE ADVANCED FOR IIT ENTRANCE )
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE MAIN AND OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((C ) MULTIPLE CHOICE QUESTION WITH MORE THAN ONE CORRECT ANSWER)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((D ) MULTIPLE CHOICE QUESTION BASED ON A GIVEN PASSAGE/COMPREHENSION )
- CONCEPTUAL QUESTIONS
- HIGH ORDER THINKING SKILLS AND ADVANCED LEVEL
- NCERT FILE (TEXTBOOK EXERCISE)
- PRACTICE PROBLEM
- REVISION EXERCISE (ADDITIONAL QUESTION)
- REVISION EXERCISE (FILL IN THE BLANKS)
- REVISION EXERCISE (LONG ANSWER QUESTION)
- REVISION EXERCISE (NUMERICAL PROBLEM)
- REVISION EXERCISE (SHORT ANSWER QUESTION)
- REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
- SOLVED EXAMPLE
- TOUGH AND TRICKY PROBLEM