Three rods of equal length and equal area of cross section are connected end to end in series. The open end of the first rod (from left) is at a temperature of 300∘C and that of the last rod is at 20∘C in steady state. If the thermal conductivities of rods from left to right are in the ratio of 1: 3: 4, then find the temperatures of both the junctions.
To solve the problem of finding the temperatures at the junctions of three rods connected in series, we can follow these steps:
Step 1: Understand the Setup
We have three rods connected in series, with the following conditions:
- The temperature at the left end of the first rod is T0=300∘C.
- The temperature at the right end of the last rod is T3=20∘C.
- The thermal conductivities of the rods are in the ratio 1:3:4.
Let the thermal conductivities of the rods be:
- k1=k (for the first rod)
- k2=3k (for the second rod)
- k3=4k (for the third rod)
Step 2: Set Up Heat Flow Equations
In steady state, the heat flow through each rod is the same. We can express the heat flow Q through each rod using the formula:
Q=k⋅A⋅(Thot−Tcold)L
where A is the area of cross-section, L is the length of the rods, and Thot and Tcold are the temperatures at the ends of the rod.
For the first rod:
Q=k⋅A⋅(300−T1)L
For the second rod:
Q=3k⋅A⋅(T1−T2)L
For the third rod:
Q=4k⋅A⋅(T2−20)L
Step 3: Equate the Heat Flow
Since the heat flow is the same through all three rods, we can set the equations equal to each other:
1. From the first and second rods:
k⋅A⋅(300−T1)L=3k⋅A⋅(T1−T2)L
2. From the second and third rods:
3k⋅A⋅(T1−T2)L=4k⋅A⋅(T2−20)L
Step 4: Simplify the Equations
We can cancel k, A, and L from all equations since they are common factors.
1. Simplifying the first equation:
300−T1=3(T1−T2)
Expanding gives:
300−T1=3T1−3T2
Rearranging leads to:
4T1−3T2=300(Equation 1)
2. Simplifying the second equation:
3(T1−T2)=4(T2−20)
Expanding gives:
3T1−3T2=4T2−80
Rearranging leads to:
3T1−7T2=−80(Equation 2)
Step 5: Solve the System of Equations
We now have two equations:
1. 4T1−3T2=300
2. 3T1−7T2=−80
We can solve these equations simultaneously.
From Equation 1, we can express T2:
T2=4T1−3003
Substituting T2 into Equation 2:
3T1−7(4T1−3003)=−80
Multiplying through by 3 to eliminate the fraction:
9T1−7(4T1−300)=−240
Expanding gives:
9T1−28T1+2100=−240
Combining like terms:
−19T1+2100=−240
Solving for T1:
−19T1=−240−2100
−19T1=−2340
T1=234019≈123.16∘C
Step 6: Find T2
Now substituting T1 back into the equation for T2:
T2=4(123.16)−3003=492.64−3003=192.643≈64.21∘C
Final Answer
The temperatures at the junctions are:
- T1≈123.16∘C
- T2≈64.21∘C
We have three rods connected in series, with the following conditions:
- The temperature at the left end of the first rod is T0=300∘C.
- The temperature at the right end of the last rod is T3=20∘C.
- The thermal conductivities of the rods are in the ratio 1:3:4.
- k1=k (for the first rod)
- k2=3k (for the second rod)
- k3=4k (for the third rod)
In steady state, the heat flow through each rod is the same. We can express the heat flow Q through each rod using the formula:
Q=k⋅A⋅(Thot−Tcold)L
where A is the area of cross-section, L is the length of the rods, and Thot and Tcold are the temperatures at the ends of the rod.
Q=k⋅A⋅(300−T1)L
Q=3k⋅A⋅(T1−T2)L
Q=4k⋅A⋅(T2−20)L
Since the heat flow is the same through all three rods, we can set the equations equal to each other:
k⋅A⋅(300−T1)L=3k⋅A⋅(T1−T2)L
3k⋅A⋅(T1−T2)L=4k⋅A⋅(T2−20)L
We can cancel k, A, and L from all equations since they are common factors.
300−T1=3(T1−T2)
Expanding gives:
300−T1=3T1−3T2
Rearranging leads to:
4T1−3T2=300(Equation 1)
3(T1−T2)=4(T2−20)
Expanding gives:
3T1−3T2=4T2−80
Rearranging leads to:
3T1−7T2=−80(Equation 2)
We now have two equations:
1. 4T1−3T2=300
2. 3T1−7T2=−80
T2=4T1−3003
3T1−7(4T1−3003)=−80
Multiplying through by 3 to eliminate the fraction:
9T1−7(4T1−300)=−240
Expanding gives:
9T1−28T1+2100=−240
Combining like terms:
−19T1+2100=−240
Solving for T1:
−19T1=−240−2100
−19T1=−2340
T1=234019≈123.16∘C
Now substituting T1 back into the equation for T2:
T2=4(123.16)−3003=492.64−3003=192.643≈64.21∘C
The temperatures at the junctions are:
- T1≈123.16∘C
- T2≈64.21∘C
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:PRACTICE PROBLEM
Explore 28 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CONCEPTUAL QUESTIONS
Explore 16 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Chapter Practice Test (for Board Examination)
Explore 16 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Three bars of equal lengths x and equal area of cross-section A are connected in series. Their thermal conductivities are in the ratio 2:4:3. If the open ends of the first and the last bars are at temperatures 200∘C and 18∘C, respectively in the steady state, calculate the temperatures of both the junctions.
View SolutionThree bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200∘C and 180∘C respectivity in the steady state, calculate the temperature of both the junctions.
View Solution
Knowledge Check
Two rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
A80∘CB64∘CC20∘CD16∘CA rod of 1m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperature 100∘C and 0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm−1s−1('∘C)]
 A9×10−4kilocal/secB9kilocal/secC0.09kilocal/secD9×10−6kilocal/sec
A9×10−4kilocal/secB9kilocal/secC0.09kilocal/secD9×10−6kilocal/secTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)K
Three bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
 .
.
View SolutionThree rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
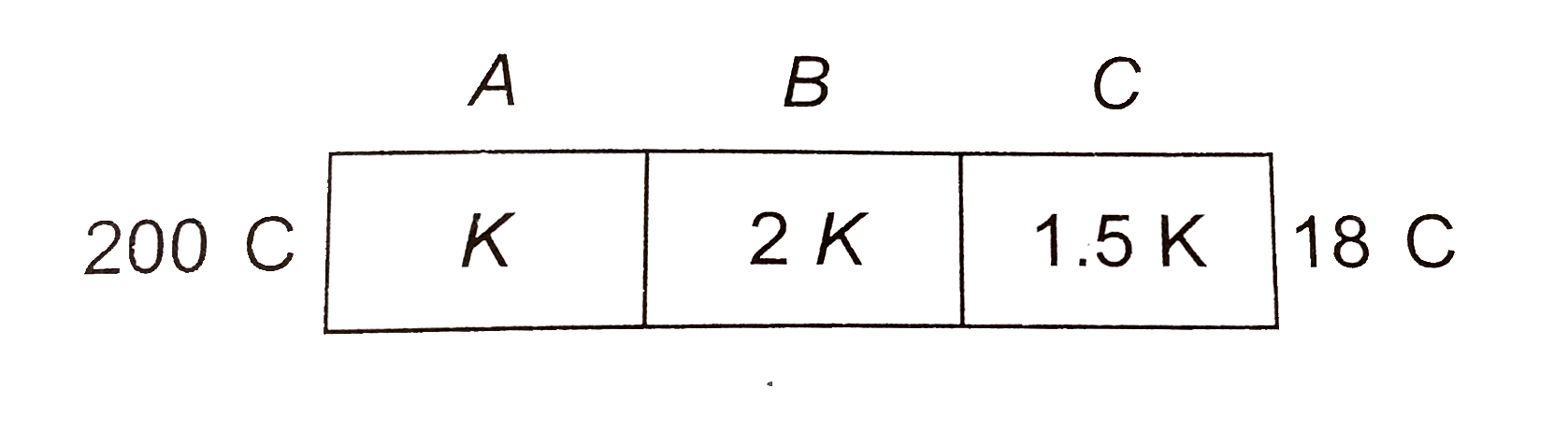
View SolutionThree rods of lengths L,21 and 3L having thermal conductivities 3K,2K and K are connected end to end If cross sectional areas of three rods are equal If cross sectional areas of three rods are equal then equivalent thermal conductivity of the system is .
View Solution

