Three bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200∘C and 180∘C respectivity in the steady state, calculate the temperature of both the junctions.
Step by step video & image solution for Three bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200^(@)C and 180^(@)C respectivity in the steady state, calculate the temperature of both the junctions. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Problems from competitive examinations
22 Videos
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Problems for self practice
97 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
- Units and MeasurementsBOOK - SL ARORACHAPTER - Units and MeasurementsEXERCISE - Exercise
499 Videos
Similar Questions
Three bars of equal lengths x and equal area of cross-section A are connected in series. Their thermal conductivities are in the ratio 2:4:3. If the open ends of the first and the last bars are at temperatures 200∘C and 18∘C, respectively in the steady state, calculate the temperatures of both the junctions.
View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
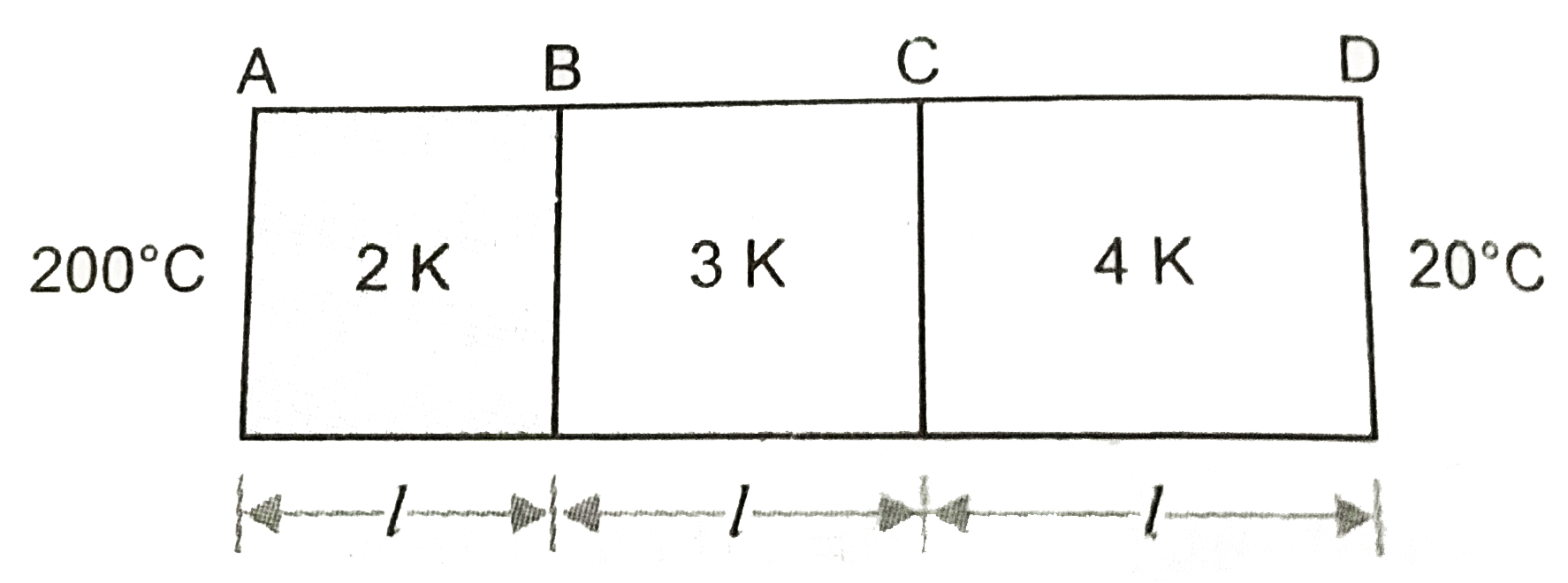 .
.
View Solution
Knowledge Check
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
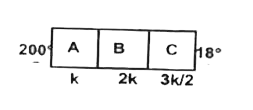 A156∘CB148∘CC116∘CD74∘C
A156∘CB148∘CC116∘CD74∘CThree bars each of area of cross section A and length L are connected in series as shown in the figure. Thermal conductivities of their materials are K, 2K and 1.5K. If the temperatures of free end of first and the last bar are 200∘C and 18∘C. The value of θ1 and θ2 are (in steady state):
A120∘C,80∘CB116∘C,80∘CC116∘C,74∘CD120∘C,74∘CTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
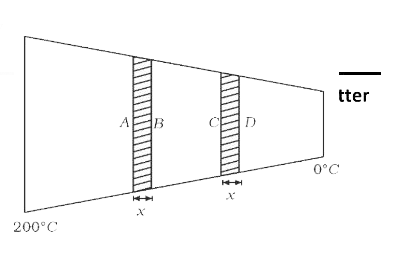 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
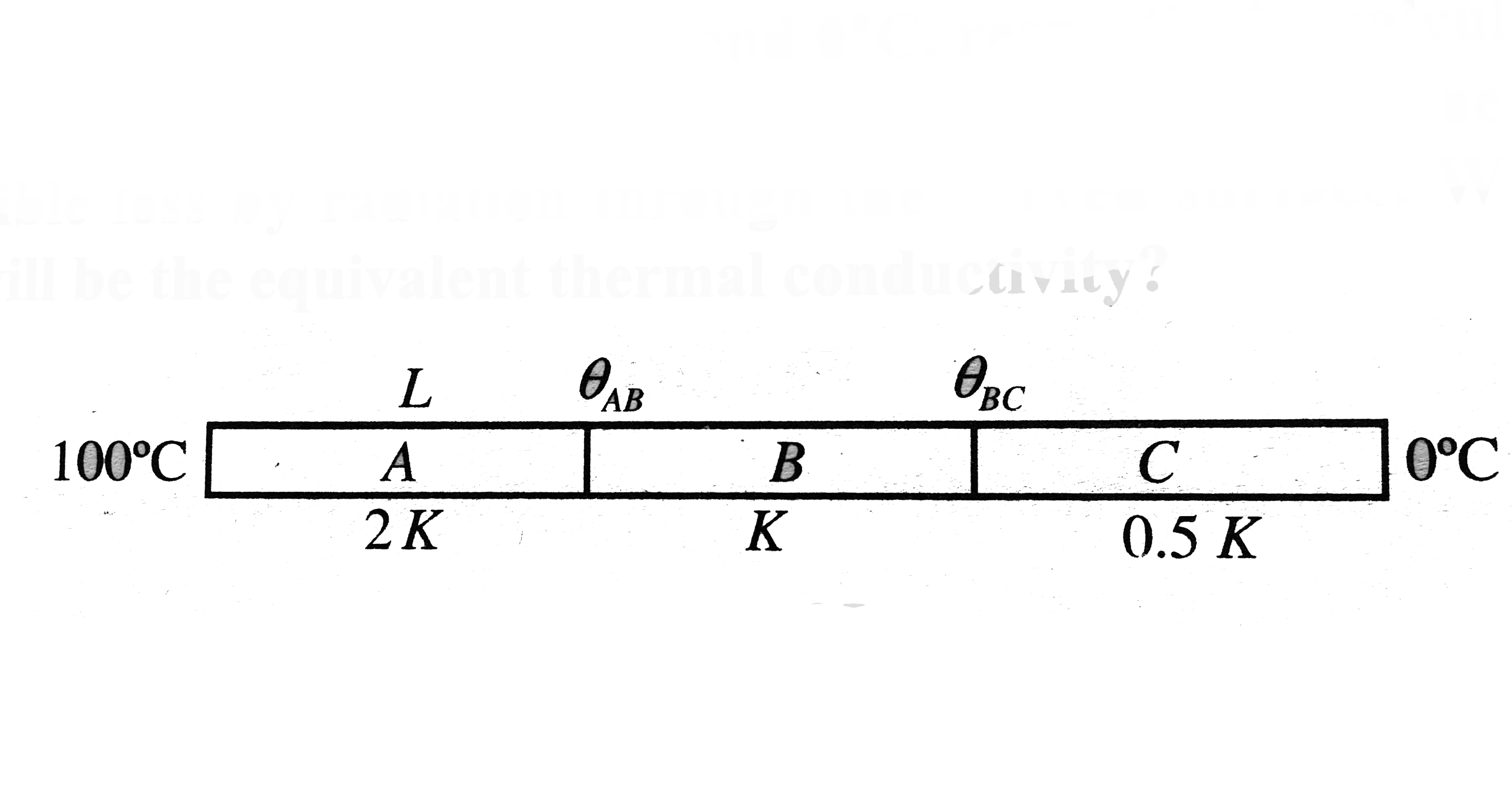
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View SolutionThree rods of equal length and equal area of cross section are connected end to end in series. The open end of the first rod (from left) is at a temperature of 300∘C and that of the last rod is at 20∘C in steady state. If the thermal conductivities of rods from left to right are in the ratio of 1: 3: 4, then find the temperatures of both the junctions.
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionThree metal rods of same lenghs and same area of cross sections having conductivities 1,2,3, units are connected in series Then their effective conductivity will be .
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View Solution
