Complete Solutions to PRACTICE PROBLEM of chapter THERMAL PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMAL PROPERTIES OF MATTER |
| MODERN PUBLICATION | PRACTICE PROBLEM |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
A Fahrenheit thermometer and a Celsius thermometer are put in a hot liquid in a cylinder. The reading on Celsius scale is `3/2` times the reading on Fahrenheit scale. Calculate the temperature on Celsius, Fahrenheit and Kelvin Scale.
View SolutionA thermometer has wrong calibrations marked on it. The lower and upper fixed points on it are `4^@` and `96^@` . The temperature of a body measured by this thermometer is `60^@` . Calculate the correct temperature of the body on Celsius scale.
View SolutionA faulty thermometer reads melting point of ice as` -5 ^@C` and it reads `70^@C` instead of `60^@C` . What will be temperature of boiling point of water on this scale?
View SolutionThe pressure recorded by a constant volume gas thermometer is `3.1 xx10^4` Pa at melting point of sulphur and `1.8 xx 10^4` Pa at triple point of water. What will be melting point of sulphur?
View SolutionSmall amount of mercury is poured in a glass container of 2 litres capacity. Calculate the volume of mercury in the container assuming that volume of air inside the container always remains same.
`alpha` for glass ` = 9 xx 10^(-6)""^@C^(-1)`
`alpha` for mercury ` = 0.6 xx 10^(-4) ""^@C^(-1)`
View SolutionIn a certain arrangement, two cylinders of brass and steel are laid side by side and there is a constant difference of length between them at any temperature. Calculate the lengths of these cylinders at `0^@C` if there is a difference of 5 cm between their lengths at all temperatures.
`alpha_("brass") = 0.0000019^@C^(-1)`
` alpha_("steel") = 1.2 xx 10^(-6) C^(-1)`
View SolutionA clock with a steel pendulum gives accurate time at `30^@C` . Calculate the fractional loss or gain in time if temperature changes to `50^@C` . Coefficient of linear expansion of steel `= 12 xx 10^(-6) ""^@C^(-1)`
View SolutionA metallic sphere is heated from 225 K to 325 K. On heating, the volume increases by 2% of original value. Find the coefficients of linear, superficial and cubical expansion of metal.
View SolutionCalculate the volume of ethane required to be burnt to convert 100 kg of water at `20^@C` to steam at `100^@C` , assuming that only 40% of heat is useful. Heat of combustion of ethane is 371 kcal `"mol"^(-1)` . (One mole of gas occupies 22.4 litres at S.T.P. and latent heat of water is `2.25 xx 10^6 J kg^(-1)` )
View Solution100 gm of water at `20^@C` is converted into ice at `0^@C` by a refrigerator in 2 hours. What will be the quantity of heat removed per minute? Specific heat of water = `1 cal g^(-1) C^(-1) ` and latent heat of ice `= 80 cal g^(-1)`
View SolutionOn mixing 0.35 kg of ice at `0^@C` with 0.8 kg of water at `45^@C` in a container, the final temperature becomes `20^@C` . What will be the heat of fusion of ice? (Specific heat of water `= 4186 J kg^(-1) K^(-1)` )
View SolutionA room is to be maintained at a constant temperature of `30^@C` and is heated by a heater of resistance `10 Omega ` connected to 210 V mains supply. Heat is transmitted outside through a window of thickness 0.3 cm and area `2 m^2` What will be temperature outside the window?
Thermal conductivity of glass `= 0.3 cal s^(-1) m^(-1) ""^@C^(-1)`
View SolutionA rectangular steel tank of thickness 3 cm contains water. The water in the tank is boiled by a furnace. The level of water falls at a constant rate of 1.5 cm in 15 minutes. What will be the temperature of furnace if K for steel is `0.2 cal s^(-1) m^(-1) ""^@C^(-1)` ?
View SolutionThree rods made of same material and having same cross-section have been joined as shown in Fig. 7(e).18. Each rod is of the same length. The left and the right ends are kept at `0^(@)C` and `60^(@)C` respectively. What is the temperature of the junction of the three rods.
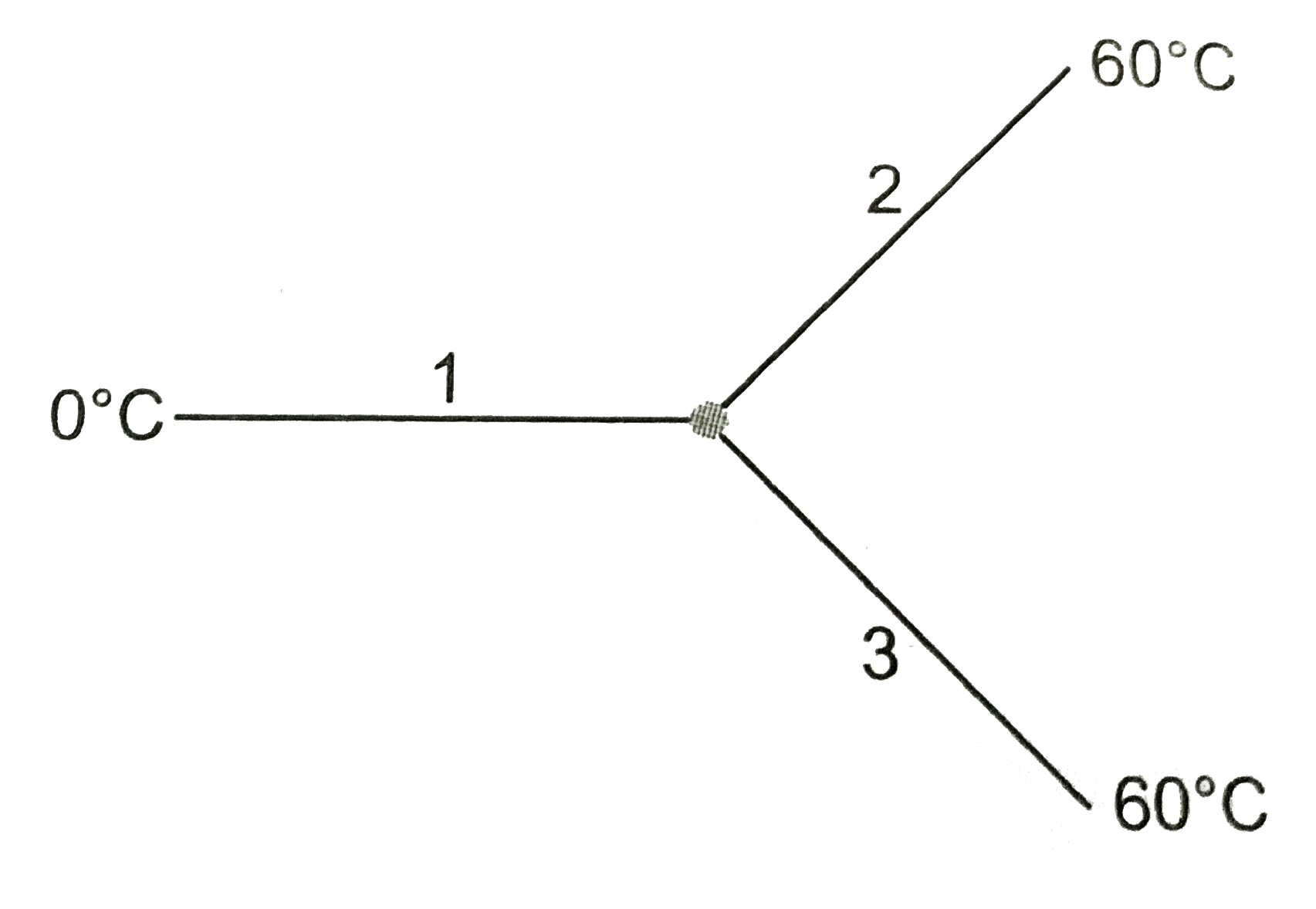
View SolutionThe temperature difference between two ends of a 2 m long bar A is `40^@C` and that between a 3 m long bar B of same area is `60^@C` . If the rate of conduction of heat in two bars is same, calculate the ratio of coefficients of thermal conductivity of two bars.
View SolutionAn ice layer of thickness 3 cm is formed on a lake. How much time will it take to increase the thickness of ice by 2 mm if temperature of air is `-30^@C` ? Take, Density of ice `= 1 g cm^(-3) ` , Latent heat of ice `= 80 cal g^(-1) ` , Conductivity of ice `= 0.008 cal s^(-1) cm^(-1) ""^@C^(-1)`
View SolutionA body cools from `70^@C` to `60^@C` in 10 minutes. Calculate the temperature of body after further 7 minutes if temperature of surroundings is `12^@C` .
View SolutionA pan filled with hot food cools from `50^@C` to `40^@C` in 2 minutes and to `30^@C` in next 5 minutes. Calculate the temperature of surroundings.
View SolutionA body cools from `90^@C` to `80^@C` in 2 minutes. How long will it take to cool from `70^@C` to `50^@C` if temperature of surroundings is `16^@C` ?
View SolutionAn electric heater is made up of 10 thin polished tubes of a metal. Each tube is 0.5 m long and 2 cm in diameter. Hot water at `60^@C` is constantly circulating through the tubes. What will be the heat radiated in 2 hours by the heater in a room where room temperature is `16^@C` ? Take, Emissivity of metal `= 5 xx 10^(-2)` and ` sigma = 5.67 xx 10 Js^(-1)m^(-2) K^(-4)`
View SolutionThe initial temperature of a black body is `527^@C`. What should be its temperature so as to double the emitted radiations?
View SolutionAn energy radiator at `0^@C` is radiating energy at the rate of `2.2 xx 10^4 erg cm^(-2)s^(-1)` . Calculate the heat radiated per second by a spherical body of radius 2 cm and at a temperature of `100^@C` .
`sigma = 5.67 xx 10^(-5) erg cm^(-2) s^(-1) K^(-4)`
View SolutionA hot body at `800^@C` is radiating 500 J of energy per minute. Calculate the surface area of the body if emissivity is 0.23 and Stefan's constant is `5.67 xx 10^(-8) Wm^(-2) K^(.-4)` .
View SolutionThe surface temperature of the hot body is `1127^(@)C` find the wavelenght at which it radiates maximum energy. Given Wien's constant = 0.2898 cm K. To which spectrum region this wavelength belongs?
View SolutionThe maximum wavelength observed in the spectral energy distribution of sun is at 4673 Å, at a temperature of about 6000 K. For a star, this maximum is at 9000 Å. Calculate the temperature of the star.
View SolutionThe thermal emissivities of two bodies A and B are 0.02 and 0.09, respectively. `lamda_A` and `lamda_B` are the wavelengths corresponding to maximum intensity of radiations and `lamda_A` is shifted from `lamda_B` by ` mu m` . If the surface area and the total power radiated by the bodies are same, then calculate the temperature of B, given temperature of A is 5000 K.
View SolutionCalculate the electrical energy consumed per second in an electric bulb with tungsten filament of area `0.35 cm^2` when its temperature is raised to 2000 K, by passing an electric current through it. The emissivity of filament is 0.45. Stefan's constant, `sigma = 5.67 xx 10^5 erg s^(-1) cm^(-2) K^(-4)`
View SolutionA sphere with radius 10 cm is radiating 500 W power at 700 K. Calculate the power radiated if radius of sphere is doubled and temperature is halved.
View Solution
PRACTICE PROBLEM questions and complete solutions for chapter THERMAL PROPERTIES OF MATTER of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS THERMAL PROPERTIES OF MATTER
- CHAPTER PRACTICE TEST
- COMPETITION FILE (ASSERTION REASON TYPE QUESTION )
- COMPETITION FILE (EXEMPLAR PROBLEM OBJECTIVE TYPE QUESTION (MULTIPLE CHOICE QUESTION TYPE - I )
- COMPETITION FILE (EXEMPLAR PROBLEM OBJECTIVE TYPE QUESTION (MULTIPLE CHOICE QUESTION TYPE - II )
- COMPETITION FILE (EXEMPLAR PROBLEM SUBJECTIVE QUESTION (SHORT ANSWER TYPE QUESTION)
- COMPETITION FILE (EXEMPLAR PROBLEM SUBJECTIVE QUESTION (VERY SHORT ANSWER TYPE QUESTION)
- COMPETITION FILE (INTEGER TYPE QUESTION )
- COMPETITION FILE (MATRIX MATCH TYPE QUESTION )
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((A) MULTIPLE CHOICE QUESTION WITH ONLY ONE CORRECT ANSWER))
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) AIMPMT/NEET AND OTHER STATE BOARDS FOR MEDICAL ENTRANCE)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE ADVANCED FOR IIT ENTRANCE )
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE MAIN AND OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((C ) MULTIPLE CHOICE QUESTION WITH MORE THAN ONE CORRECT ANSWER)
- COMPETITION FILE (OBJECTIVE TYPE QUESTION ((D ) MULTIPLE CHOICE QUESTION BASED ON A GIVEN PASSAGE/COMPREHENSION )
- CONCEPTUAL QUESTIONS
- HIGH ORDER THINKING SKILLS AND ADVANCED LEVEL
- NCERT FILE (TEXTBOOK EXERCISE)
- PRACTICE PROBLEM
- REVISION EXERCISE (ADDITIONAL QUESTION)
- REVISION EXERCISE (FILL IN THE BLANKS)
- REVISION EXERCISE (LONG ANSWER QUESTION)
- REVISION EXERCISE (NUMERICAL PROBLEM)
- REVISION EXERCISE (SHORT ANSWER QUESTION)
- REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
- SOLVED EXAMPLE
- TOUGH AND TRICKY PROBLEM