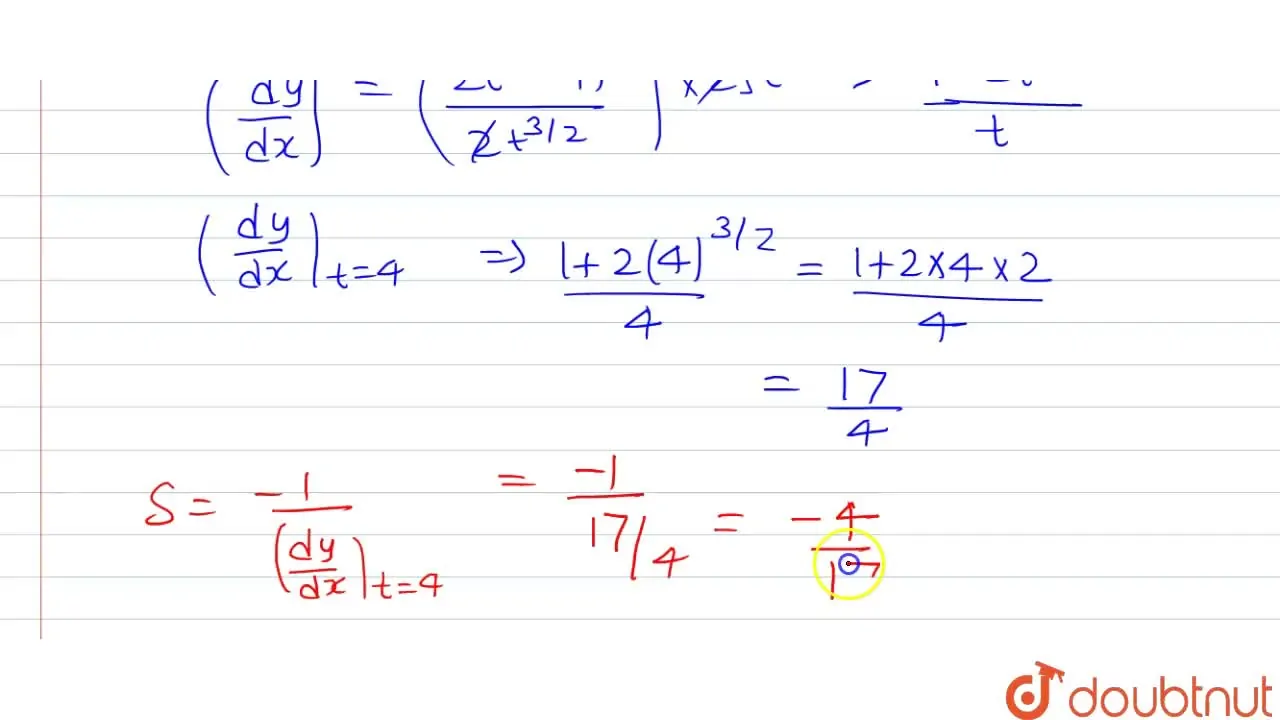The slopee of normal to the curve x=√tandy=t−1√t at t=4 is . . .
A
−174
B
417
C
−417
D
174
Video Solution
Text Solution
The correct Answer is:C
We have, x=√tandy=t−1√t
Now, dxdt=12√t,dydt=1+12t−3/2
∴dydx=dydtdxdt=1+12t−3/212√t=2√t(1+12t−3/2)
=2√t(1+12t3/2)=2t3/2+1t
At t=4,dydx=2(4)3/2+14=174
∴ Slope of normal at t=4,−1(dydx)=−417
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The equation of normal to the curve x=1t,y=t−1t at t=2 is
View SolutionEquations of the tangent and normal to the curve x=√t,y=t−1√t at the point t=4 are respectively
View SolutionThe equation of tangent to the curve x=1t,y=t−1t at t=2 is
View SolutionEquation of the tangent and normal to the curve x=1t,y=t−1t at the pint t=2 on it are respectively
View SolutionThe length of the normal to the curve x= a(t +sin t),y = a(1-cos t), "at" t= pi// 2 is
View SolutionFind the equation of normal to the curves x=t2,y=2t+1 at point
View SolutionThe length of the normal at t on the curve x=a(t+sint),y=a(1−cost), is
View Solutionx=√sin2t,y=√cos2t
View SolutionThe slove of the normal to the curve given by x=f(t),y=g(t) at the point where t=t0 is
View SolutionThe slope of the tangent to the curve x=1t,y=t−tt, at t=2 is ………….
View Solution