If z=ax+by,a,b,>0 subject to x≤2,y≤2,x+y≥3,x≥0,y≥0 has minimum value at (2,1) only, then . .
A
a>b
B
a=b
C
a<b
D
a=1+b
Video Solution
Text Solution
The correct Answer is:C
We have, z=ax+by,a,b>0
Subject to constrants x≤2,y≤2,x+y≥3x,y≥0
On taking given constraints are equation, we get the following graph
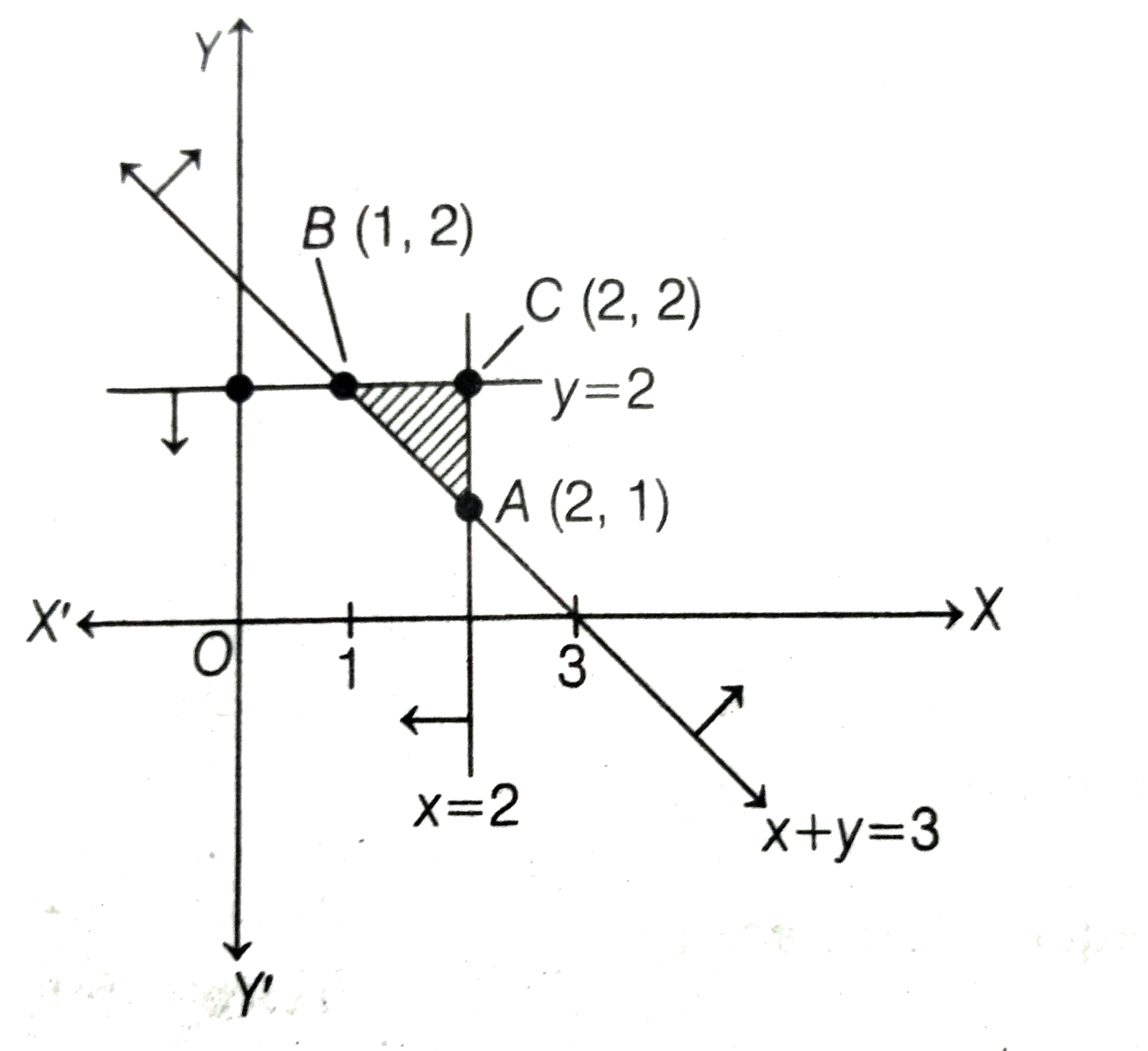
here, ABCA is the required feasible region whose corner ponts are A(2,1), B(1,2) and C(2,2).
Since, it is given that z=ax+by, a,bgt0
has minimum value at (2,1).
∴Value of z at (2,1)ltvalue of z at (1,2)
⇒2a+b<a+2b
⇒a<b
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Minimise z=3x+y, subject to 2x+3y≤6,x+y≥1,x≥0,y≥0
Ax=1,y=1Bx=0,y=1Cx=1,y=0Dx=−1,y=−1If 4x+5y≤20,x+y≥3,x≥0,y≥0 maximum 2x + 3y is
A12B5C0D20The maximum value of z=4x+6y subject to 3x+2y≤12,x+y≥4,x≥0,y≥0 is
A36B16C24D38
The minimum value of z=7x+y subject to 5x+y≥5,x+y≥3,x≥0,y≥0 is
View SolutionMax value of z equal 3x + 2y subject to x+y≤3,x≤2,−2x+y≤1,x≥0,y≥0 is
View SolutionThe minimum value of z=2x+4y subject to x+2y≥2,3x+2y≥6,x≥0,y≥0 is
View SolutionMaximise Z=2x+3y subject to x+2y≤6,x≥4,y≥0 is :
View SolutionThe maximum value of z=6x+4y subject to x≤2,x+y≤3,−2x+y≤1,x≥0,y≥0, is
View Solution
