A player tosses 2 fair coins. He wins Rs. 5 if 2 heads appear, Rs. 2 if 1 head appear and Rs. 1 if no head appears, then variance of his winning amount is
6
52
94
172
The correct Answer is:C
When player tosses 2 fair coins then
S={HT,TH,TT,HH}
Let X be a random variable that denotes the amount received by the player,
Then, X can take value 5,2 and 1. P(X=5)=14,P(X=2)=24=12
and P(X=1)=14
Thus, the probability distribution of X is
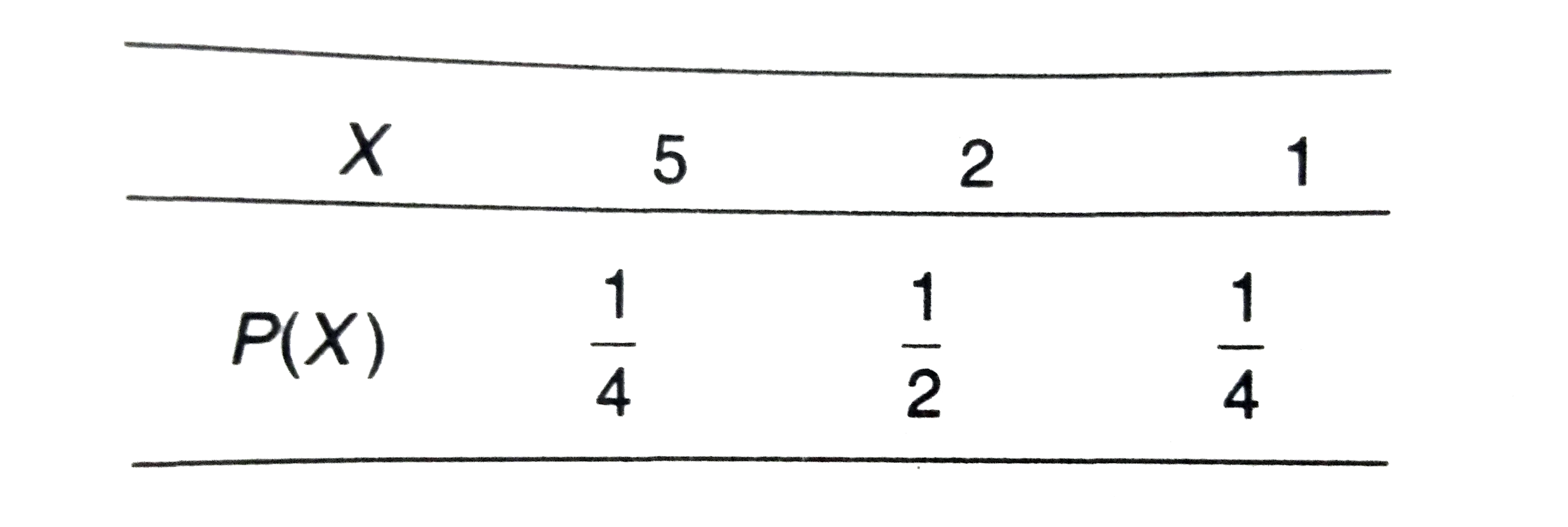
∴Variance of X=∑X2P(X)−[∑XP(X)]2
Now, ∑XP(X)=5×14+2×12+1×14
=54+44+14=104=52
∴Variance off X=∑X2P(X)−(∑XP(X))2
=(25×14+4×12+1×14)−(52)2
=(25+8+14)−254=94
Topper's Solved these Questions
Similar Questions
A player tosses two coins he wins Rs.10 if 2 heads appears , Rs. 5 if 1 head appears and Rs.2 if no head appears. Find the expected winning amount and variance of winning amount.
View SolutionA player tosses 2 fair coins. He wins 5 if 2 heads apper , 2if 1 head appers and 1 if no head appers. Find his expected winning amount and variance of winning amount .
View Solution
Knowledge Check
- Question 1 - Select One
A players tosses 2 fair coins. He wins Rs. 5 if 2 heads appear, Rs. 2 if 1 head appear and Rs. 1 if no head appears. Then his expected wining amount is
ARs. 1.25BRs. 2.15CRs. 2.5DRs. 2.25 - Question 2 - Select One
A boy tosses faiir coin 3 times. If he gets Rs 2X for X heads, then his expected gain equals to Rs…..
A1B32C3D4 - Question 3 - Select One
A coin is tossed three times. Consider the following events:
A: No head appears
B: Exactly one head appears
C: At least two heads appear
Which one of the following is correct?AA. (A∪B)∩(A∪C)=B∪CBB. (A∩B)∪(A∩C)=B∪CCC. A∩(B∪C)=A∪B∪CDD. A∩(B'∪C')=B'∩C'
A coin is tossed thrice. X denotes the no. of heads appeared. Find the mean and variance of X.
View SolutionTwo coins are tossed simultaneously 300 times and it is found that two heads appeared 135 times, one head appeared 111 times and no head appeared 54 times. If two coins are tossed at random, what is the probability of getting (i) 2 heads (ii) 1 head (iii) 0 head?
View SolutionA box contains three coins two of them are fair and one two-headed. A ceim is selected atrandom and tossed. If the head appears the coin is tossed again, if a tail appears, then amerlercoin is selected from the remaining coins and tossed. (i) Find the probability that head appears twice.(ii) If the same coin is tossed twice. find the probability that it is two headed coin.(iii) Find the probability that tail appears twice.
View SolutionA coin is tossed three times, consider the following events.
A : No head appears,
B: Exactly one head appears’ and
C: Atleast two appear
Do they form a set of mutually exclusive and exhaustive events?View SolutionA fair coin is tossed. If head appears, a fair dice is tossed once and the number on the upper face noted. If tail appears, the fair dice is tossed twice independently and the sum on the upper faces is noted. Then the probability that the noted number is 3, is
(A)1/18 (B)1/4 (C)1/6 (D)1/9View Solution

