The acute angle between lines x-3=0 and x+y=19 is . . .
A
60∘
B
30∘
C
90∘
D
45∘
Video Solution
Text Solution
The correct Answer is:D
Given lines are
x-3=0
slope of line (i), m1=∞⇒tanθ1=∞⇒θ1=90∘
and x+y=19
⇒y=−x+19
Slope of line (ii), m2=tanθ2=−1
∴θ=135∘
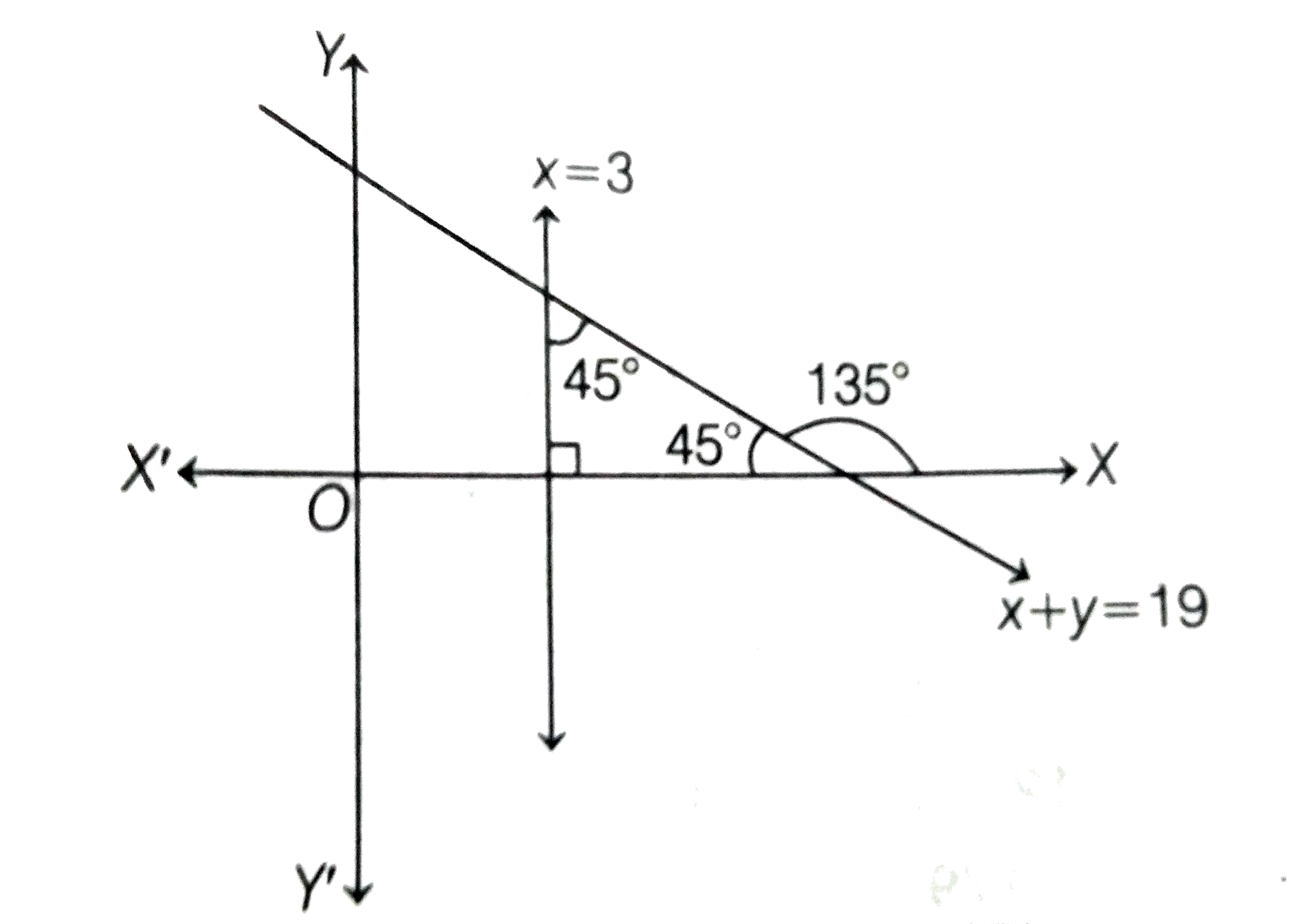
∴Acute angle between given lines is 45∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Equation of the bisector of the acute angle between lines 3x+4y+5=0 and 12x-5y-7=0 is
A21x+77y+100=0B99x-27y+30=0C99x+27y+30=0D21x-77y-100=0The angle between the lines2x−y+3=0 and x+2y+3=0 is
A90∘B60∘C45∘D30∘The angle between the lines x+y-3 =0 and x-y+3=0 is α and the acute angle between the lines x−√3y+2√3=0and√3x−y+1=0isβ which one of the following is correct?
Aα=βBα>βCα<βDα=2β
Find the bisector of acute angle between the lines x+y−3=0and7x−y+5=0
View SolutionFind the acute angle between the lines 2x−y+3=0 and x+y+2=0.
View SolutionWhat is the acute angle between the lines x−2=0 and √3x−y−2=0?
View SolutionThe angle between the lines x+y−3=0 and x−y+3=0 is α and the acute angle between the lines x−√3y+2√3=0 and √3x−y+1=0 is β which one of the following is correct?
View SolutionThe equation of the bisector of the acute angles between the lines 3x-4y+7 = 0 and 12 x + 5y -2 = 0 is :
View Solution