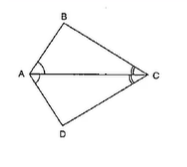
Prove that the diagonals of quadrilateral ABCD,AC
and BD
intersect in O.
Prove that if BO=OD,
the triangles ABC
and ADC
are equal in area.
In∠ABD
OB=OD
O is the midpoint of BD
AD is the median
ar(∠AOB)=ar(∠AOD)−(1)
In∠CBD
OB=OD
O is the midpoint, OC is the median
ar(∠COB)=ar(/−COD)−(2)
ar(∠AOB)+ar(∠COB)=ar(∠AOD)+ar(∠COD)
ar(∠ABC)=ar(∠ACD).
Related Playlists
Similar Questions
The diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
 View Solution
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View Solution


