The area of the triangle formed by the coordinates axes and a line is 6 square units and the length of the hypotenuse is 5units. Find the equation of the line.
Video Solution
Text Solution
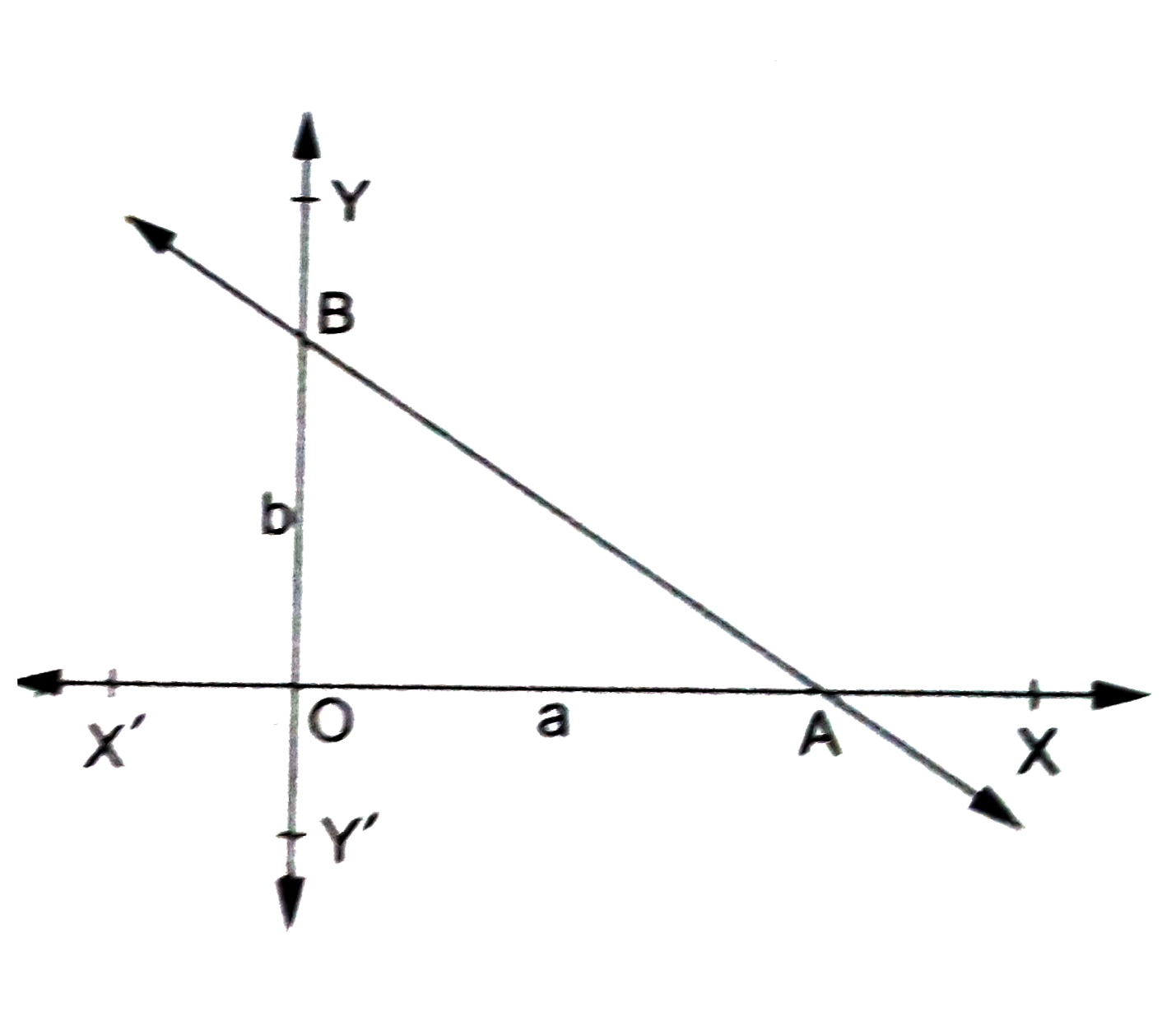
Let X'OX and YOY' be the coordinate axes, and let AB be the part of the given line intercepted by the axes.
Let the OA=a and OB=b
Then, 12,ab=6⇔ab=12….(i)
and a2+b2=25………(ii)
Putting b=12a from (i) in (ii), we get a2+144a2=25⇒a4−25a2+144=0
⇒(a2−16)(a2−9)=0⇒a2=16ora2=9
⇒a=4ora=3 [∴length is always positive]
Hence, the required equation of the line is
x4+y3=1orx3+y4=1
i.e.3x+4y−12=0or4x+3y−12=0
|
Topper's Solved these Questions
- STRAIGHT LINES Book:RS AGGARWALChapter:STRAIGHT LINES Exercise:MISCELLANEOUS PROBLEMS
Explore 9 Videos
- STRAIGHT LINES Book:RS AGGARWALChapter:STRAIGHT LINES Exercise:EXERCISE-20A
Explore 23 Videos
- STRAIGHT LINES Book:RS AGGARWALChapter:STRAIGHT LINES Exercise:EXAMPLE
Explore 56 Videos
- STATISTICSBook:RS AGGARWALChapter:STATISTICSExercise:EXERCISE 30D
Explore 5 Videos
- THREE-DIMENSIONAL GEOMETRY Book:RS AGGARWALChapter:THREE-DIMENSIONAL GEOMETRY Exercise:EXERCISE 26 C
Explore 13 Videos
Similar Questions
Knowledge Check
The area of the triangle formed by the line 5x - 3y + 15 = 0 with coordinate axes is
A15 sq. unitsB5 sq. unitsC8 sq. unitsD152 sq. unitsWhat is the area of the triangle formed by 2x+3y=6 and the coordinate axes _______. ( in sq. units)
A12B9C6D3
The area of the triangle formed by the line ax+by+c=0 with the coordinate axes is
View SolutionWrite the area of the triangle formed by the coordinate axes and the line (secθ−tanθ)x+(secθ+tanθ)y=2.
View SolutionArea of triangle formed by angular bisectors of coordinate axes and the line x=6 in sq.units is :
View SolutionThe area of the triangle formed by the line xa+yb=1 with the coordinate axes is
View SolutionFind the area of triangle formed by the line x+3y=12 with the coordinate axes.
View SolutionThe area of the triangle formed by the straight line 2x−3y+6=0 with the co-ordinate axes is (in sq.units)
View Solution

