Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Given, AB is a diameter of the circle.
A tangent is drawn from point A. Draw a chord CD parallel to the tangent MAN.

So, CD is a chord of the circle and OA is a radius of the circle.
∠MAO=90∘
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
∠CEO=∠MAO [corresponding angles]
∴∠CEO=90∘
Thus, OE bisects CD, [perpendicular from centre of circle to the radius through the point of contact]
Similarly, the diameter AB bisects all. Chords which are parallel to the tangent at the point A.
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- ARITHMETIC PROGRESSIONSBook:NCERT EXEMPLAR ENGLISHChapter:ARITHMETIC PROGRESSIONSExercise:Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
Similar Questions
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View SolutionA diameter of a circle is a chord that ..... the centre of the circle.
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
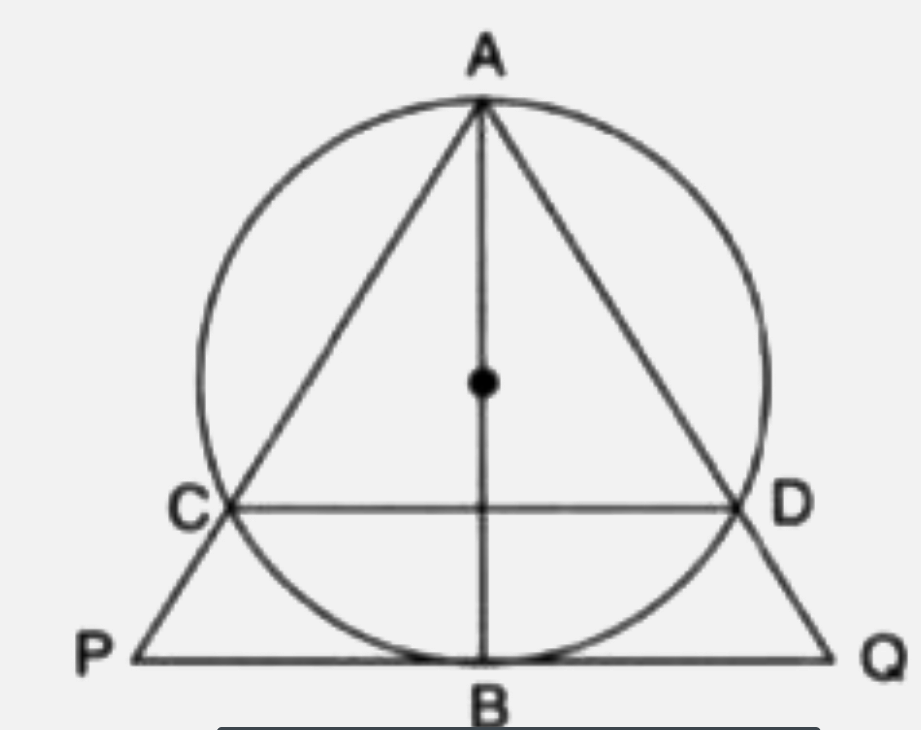
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionIn figure, tangents PQ and PR are drawn to a circle such that ∠RPQ=30∘. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
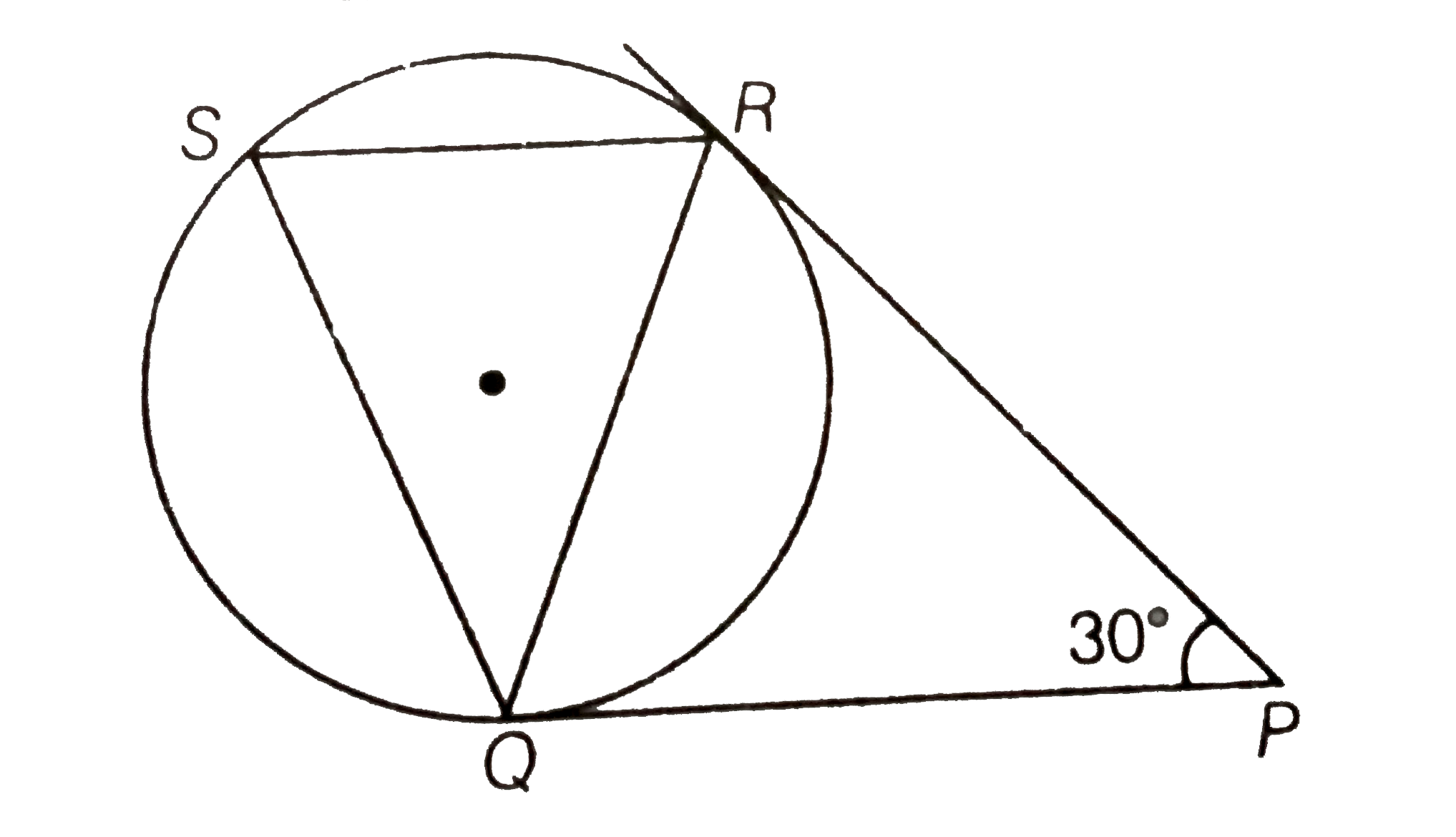
View Solution

