Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
To prove that the quadrilateral QORP is cyclic, we need to show that the sum of opposite angles is equal to 180∘.
1. Understanding the Setup:
- Let O be the center of the circle.
- PQ and PR are tangents drawn from the external point P to the circle.
- Q and R are the points of tangency on the circle.
2. Properties of Tangents:
- The tangent to a circle is perpendicular to the radius at the point of tangency.
- Therefore, ∠OQP=90∘ (since OQ is the radius and PQ is the tangent).
- Similarly, ∠ORP=90∘ (since OR is the radius and PR is the tangent).
3. Sum of Angles:
- Now, we can find the sum of the angles ∠OQP and ∠ORP:
∠OQP+∠ORP=90∘+90∘=180∘
- This shows that one pair of opposite angles in quadrilateral QORP sums to 180∘.
4. Finding the Other Pair of Angles:
- Let ∠QOR be denoted as ∠1 and ∠QPR as ∠2.
- The sum of all angles in quadrilateral QORP is 360∘:
∠OQP+∠ORP+∠QOR+∠QPR=360∘
- Substituting the known angles:
90∘+90∘+∠1+∠2=360∘
- Simplifying this gives:
180∘+∠1+∠2=360∘
- Therefore:
∠1+∠2=360∘−180∘=180∘
5. Conclusion:
- Since both pairs of opposite angles ∠OQP+∠ORP and ∠QOR+∠QPR sum to 180∘, we conclude that quadrilateral QORP is cyclic.
Final Statement:
Thus, we have proved that QORP is a cyclic quadrilateral.
---
- Let O be the center of the circle.
- PQ and PR are tangents drawn from the external point P to the circle.
- Q and R are the points of tangency on the circle.
- The tangent to a circle is perpendicular to the radius at the point of tangency.
- Therefore, ∠OQP=90∘ (since OQ is the radius and PQ is the tangent).
- Similarly, ∠ORP=90∘ (since OR is the radius and PR is the tangent).
- Now, we can find the sum of the angles ∠OQP and ∠ORP:
∠OQP+∠ORP=90∘+90∘=180∘
- This shows that one pair of opposite angles in quadrilateral QORP sums to 180∘.
- Let ∠QOR be denoted as ∠1 and ∠QPR as ∠2.
- The sum of all angles in quadrilateral QORP is 360∘:
∠OQP+∠ORP+∠QOR+∠QPR=360∘
- Substituting the known angles:
90∘+90∘+∠1+∠2=360∘
- Simplifying this gives:
180∘+∠1+∠2=360∘
- Therefore:
∠1+∠2=360∘−180∘=180∘
- Since both pairs of opposite angles ∠OQP+∠ORP and ∠QOR+∠QPR sum to 180∘, we conclude that quadrilateral QORP is cyclic.
Thus, we have proved that QORP is a cyclic quadrilateral.
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- ARITHMETIC PROGRESSIONSBook:NCERT EXEMPLAR ENGLISHChapter:ARITHMETIC PROGRESSIONSExercise:Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
Similar Questions
Two tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
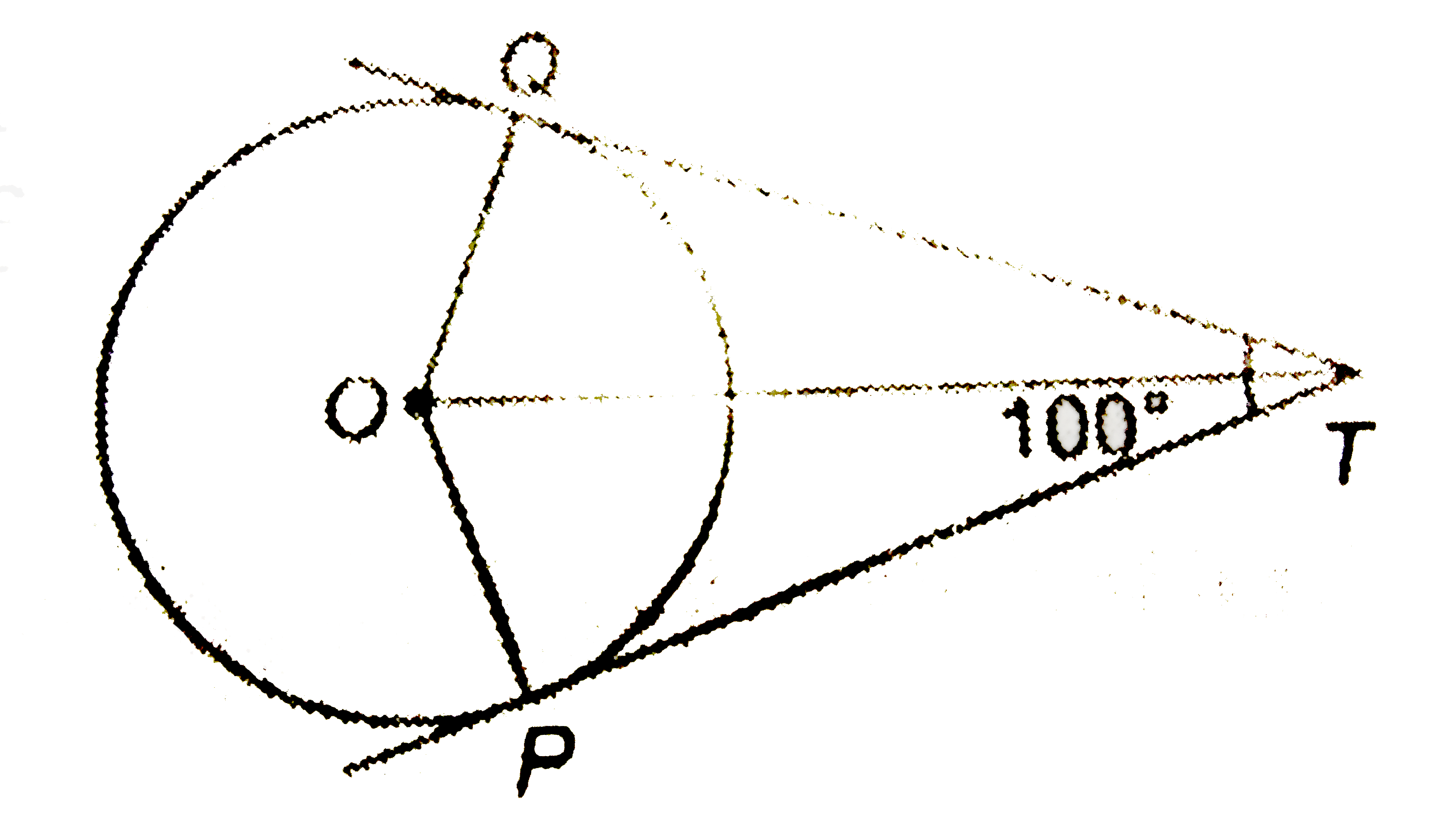
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100o , then what is the value of ∠POQ ?
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
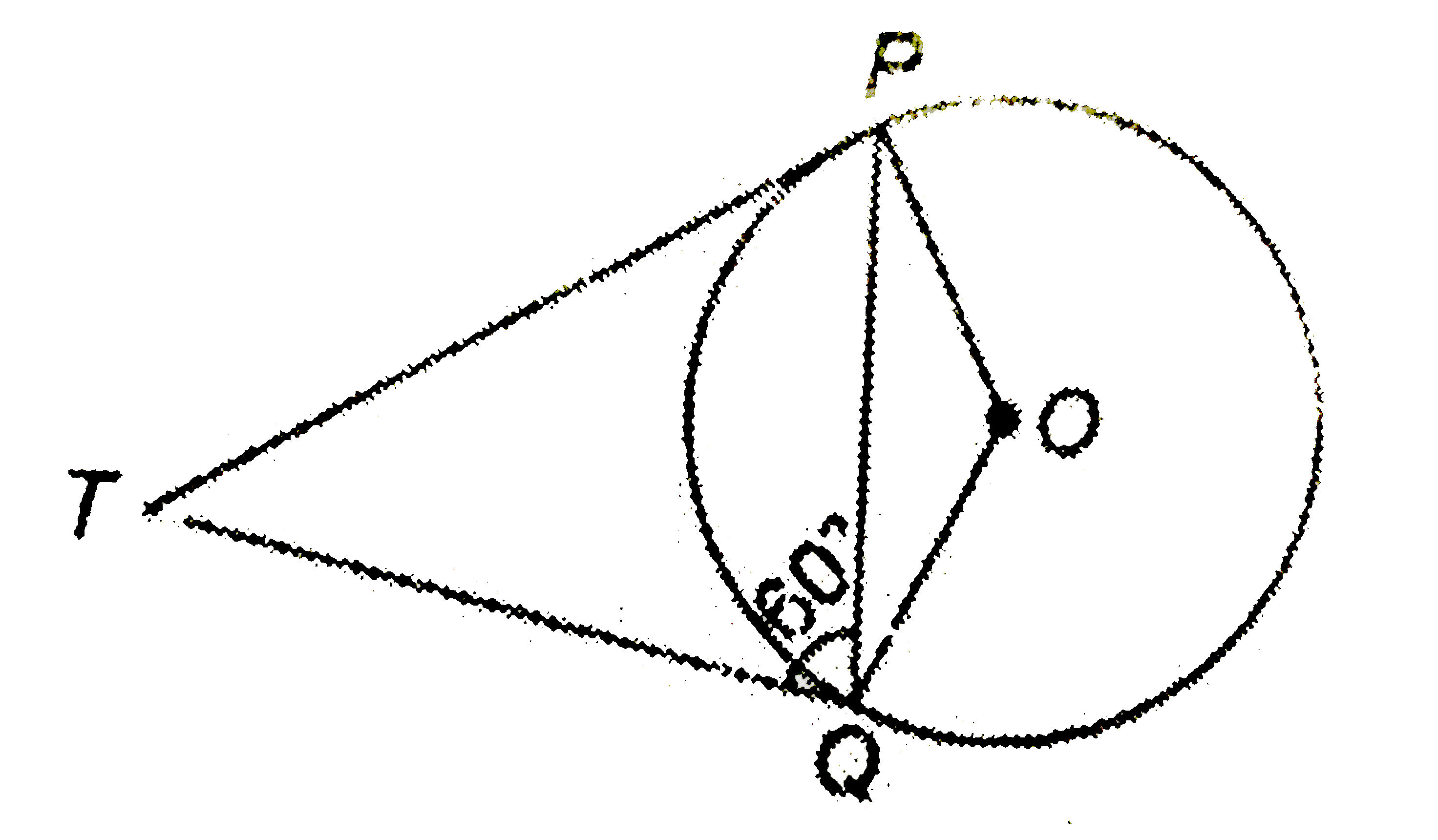
View SolutionThe length of tangent from an external point P on a circle with centre 0 is always less than OP.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution

