Let f:(0,π)→R be a twice differentiable function such that limt→xf(x)sint−f(t)sinxt−x=sin2x for all x∈(0,π).
If f(π6)=−π12, then which of the following statement (s) is (are) TRUE?
f(π4)=π4√2
f(x)<x46−x2 for all x∈(0,π)
There exists α∈(0,π) such that f'(α)=0
f'(π2)+f(π2)=0
The correct Answer is:B, C, D
Given, limt→xf(x)sint−f(t)sinxt−x=sin2x
Using L'Hospital rules
limt→xf(x)cost−f'(t)sinx1=sin2x
⇒ f(x)cosx−f'(x)sinx=sin2x
⇒ f'(x)sinx−f(x)cosx=−sin2x
⇒ f'(x)sinx−f(x)cosxsin2x=−1
⇒ d(f(x)sinx)=−1
On integrating, we get
f(x)sinx=−x+C⇒f(x)=−xsinx+Csinx
It is given that x=π6,f(π6)=−π12
∴ f(π6)=−π6sin.π6+Csin.π6=−π12=−π12+12C
⇒C=0
∴ f(x)=−xsinx
(a) f(x)=−xsinx
f(π4)=−π4sin.π4=−π4√2 false
(b) f(x)=−xsinx
sinx>x−x36,∀x∈(0,π)
⇒ −xsinx<−x2+x46
⇒ f(x)<x46−x2,∀x∈(0,π)
It is true
(c ) f(x)=−xsinx
f'(x)=−sinx−xcosx
f'(x)=0
⇒−sinx−xcosx=0
tanx=−x
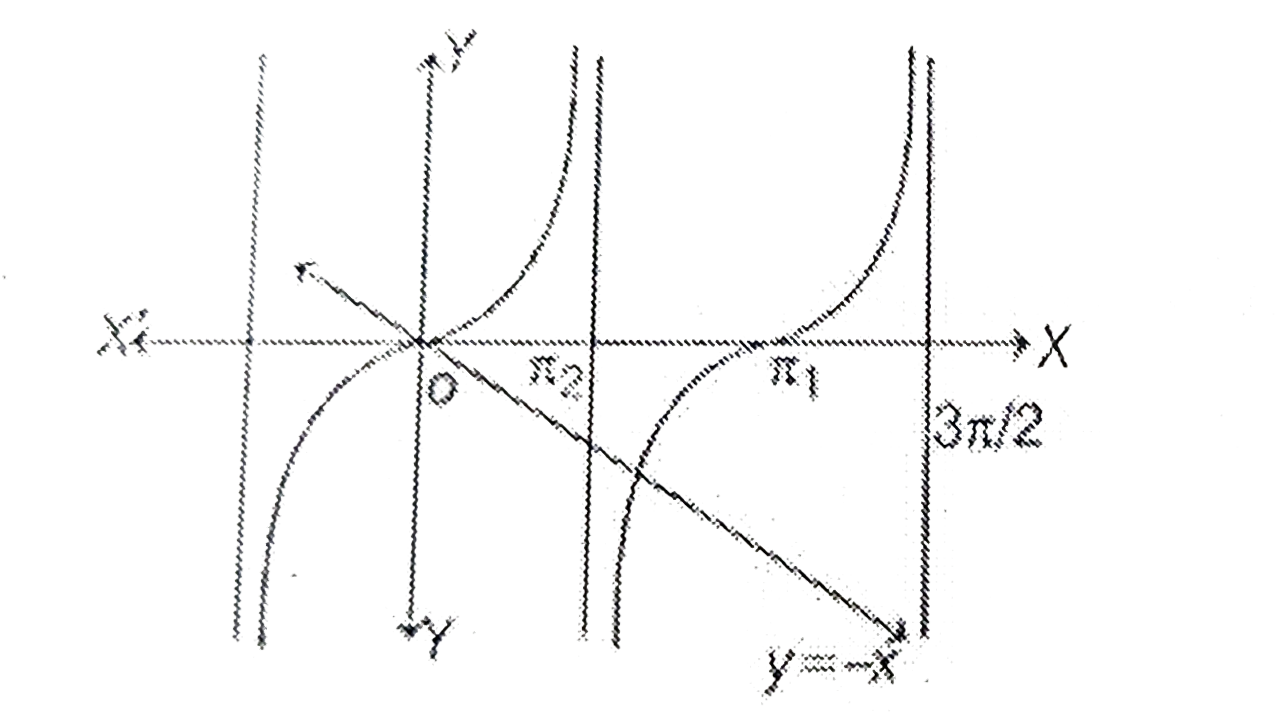
⇒Their exists α∈(0,π) for which f'(α)=0
It is true
(d) f(x)=−xsinx
f'(x)=−sinx−xcosx
f''(x)=−2cosx+xsinx
f''(π2)=π2,f(π2)=−π2
∴ f''(π2)+f(π2)=0
It is true.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point ( Assertion and Reason)1videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point (Match the Columns)2videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point ( Objective Questions I)25videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - JEE MAINSEXERCISE - All Questions1videos
JEE MAINS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)2videos
MATRICES AND DETERMINANTS
Similar Questions
Let f:(0, π)→R be a twice differentiable function such that (lim)t→xf(t)sinx−f(x)sintt−x=−sin2x for all x∈(0, π) . If f(π6)=−π12 , then which of the following statement(s) is (are) TRUE? f(π4)=π4√2 (b) f(x)<x46−x2 for all x∈(0, π) (c) There exists α∈(0, π) such that f′(α)=0 (d) f''(π2)+f(π2)=0
View SolutionLet f:R→R be a twice differentiable function such that f(x+π)=f(x) and fx+f(x)≥0 for all x∈R. Show that f(x)≥0 for all x∈R.
View SolutionLet f(x)=sin[π6sin(π2sinx)] for all x∈R
View SolutionLetf'(sinx)<0andf''(sinx)>0∀x∈(0,π2) and g(x) =f(sinx)+f(cosx)
which of the following is true?View SolutionFor tha function f(x)=(π−x)cosx|sinx|;x≠πandf(π)=1, which of the following statement is/are true :
View SolutionLet f:R→R be a differentiable function, such that f(0)=0,f(π3)=3.53. If G(x)=∫π3x(f'(t)sect+secttantf(t))dt,x∈(0,π2], then limx→∞G(x) is equal to
View Solution" f) "lim_(x rarr pi)(sin x)/(pi-x)=?
View SolutionFind the differentiable function which satisfies the equation f(x)=−∫x0f(t)tantdt+∫x0tan(t−x)dt where x∈(−π2,π2)
View SolutionIf f(x)=tan−1√1+sinx1−sinx,0≤x≤π2then f'(π6) =?
View SolutionLet f (x) be a differentiable function and satisfying the equation
f'(x)+f(x)=4xe−x.sin2xandf(0)=0 if
limn→∞n∑k=1f(kπ)=−pπeπ(eπ−1)2 then p =View Solution


