If f(x)=min.(1,x2,x3), then
A
f(x) is continuous everywhere
B
f(x) is continuous and differentiable everywhere
C
f(x) is not differentiable at two points
D
f(x) is not differentiable at one point
Video Solution
Text Solution
The correct Answer is:A, D
Here, f(x) = min {1,x2,x3} which could be graphically shown as
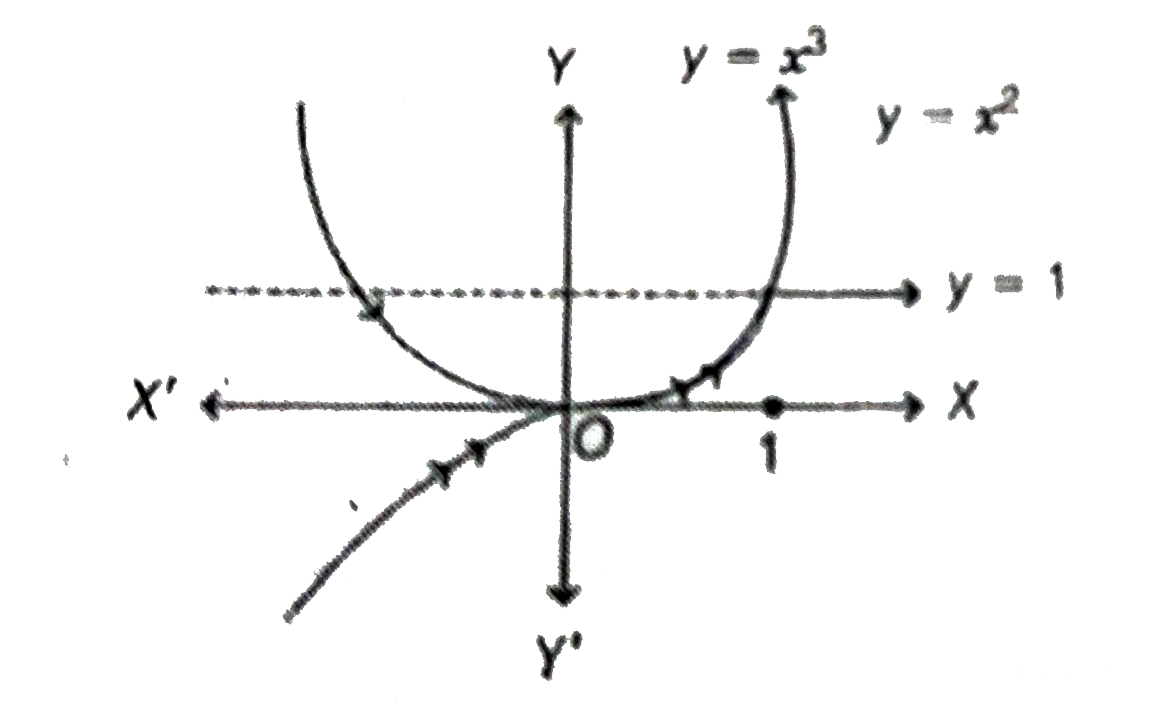
⇒ f(x) is continuous for x∈R and not differentiable at x = 1 due to sharp edge.
Hence, (a) and (d) are correct answers.
|
Topper's Solved these Questions
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point ( Assertion and Reason)
Explore 1 Video
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point (Match the Columns)
Explore 2 Videos
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point ( Objective Questions I)
Explore 25 Videos
- JEE MAINSBook:IIT JEE PREVIOUS YEARChapter:JEE MAINSExercise:All Questions
Explore 1 Video
- MATRICES AND DETERMINANTSBook:IIT JEE PREVIOUS YEARChapter:MATRICES AND DETERMINANTSExercise:SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
Explore 2 Videos
Similar Questions
Knowledge Check
If f(x)min(x,x2,x3), then
Af(x) is everywhere differentiableBf(x)>0for x>1Cf(x) is not differentiable at three points but continuous for all x∈RDf(x) is not differerntiable for two values of xLet f(x)=min{1,x2,x3}, then:
Af(x) is continous ∀x∈RBf'(x)>0,∀x>1Ccontinous but not differentiable ∀x∈RDdifferentiable everywhere
Let f(x)=min(x+1,x,1−x). Then f(2) equals
View SolutionIf f(x)={min(x,x2),x≤0andmin(2x,x2−1),x<0, then find the number of non-differentiable points of f(x).
View SolutionLet f:R→[0,1) ,where f(x)=min.({x},{−x}) ,then function
View SolutionIf f(x)=min{∣∣x2−1∣∣,|x|}, then number of extremums of f(x) in (−0.9,1.1) is
View SolutionIf f(x)=min.{−|2x−4|,x2−4}, then maximum value of f(x) is
View SolutionIf f(x)=min.{−|2x−4|,x2−4}, then maximum value of f(x) is
View Solution

