The function f (x) = 1+ $| sin x |$ is

A

continuous no where

B

continuous everywhere

C

differentiable at x = 0

D

not differentiable at infinite number of points

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

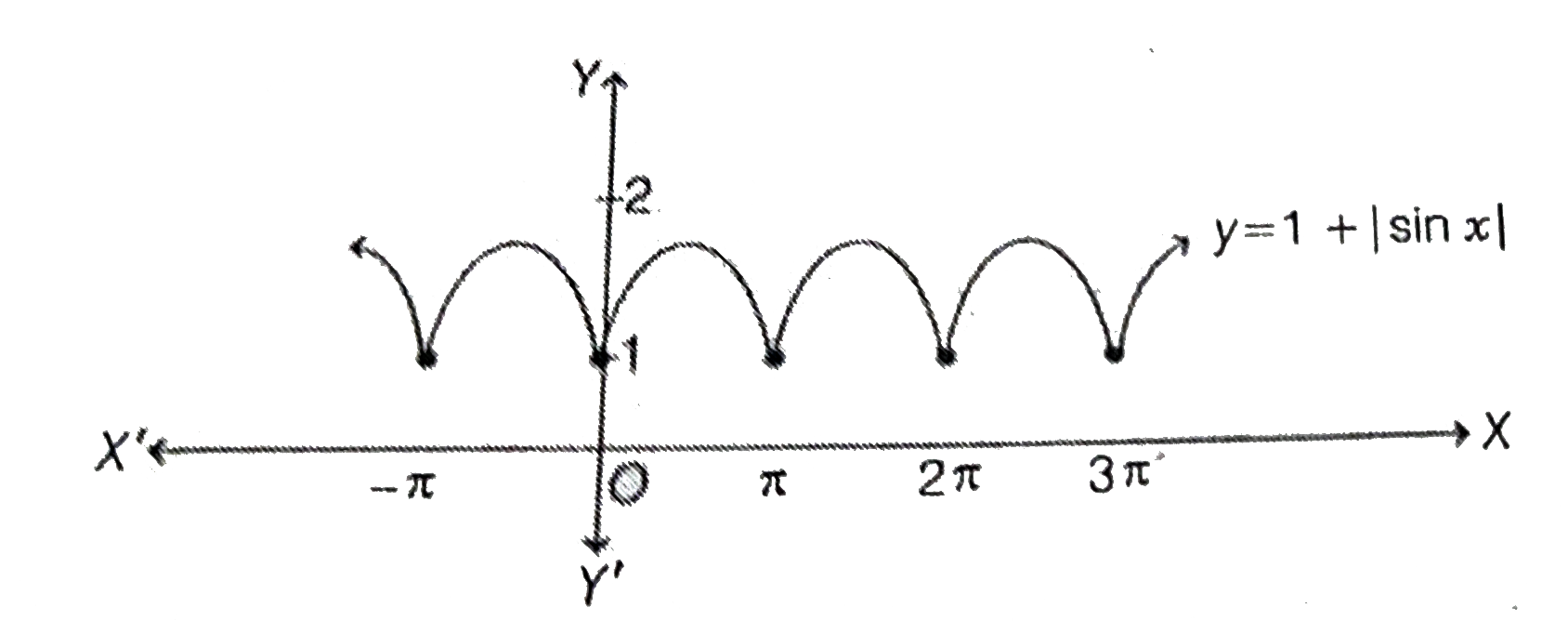
We know that, $f (x) = 1 + | sin x |$ could be plottled as,
(1) y = sin x …(i)

(2) $y = | sin x |$ …(ii)

Updated on:21/07/2023

|

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

LIMIT,CONTINUITY AND DIFFERENTIABILITY BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point ( Assertion and Reason)
1 Videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point (Match the Columns)
2 Videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point ( Objective Questions I)
25 Videos
JEE MAINSBOOK - IIT JEE PREVIOUS YEARCHAPTER - JEE MAINSEXERCISE - All Questions
1 Videos
MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos

Similar Questions

Knowledge Check

The function $f (x) = 1 + x (sin x) [cos x], 0 < x \leq \frac{π}{2}$ (where [.] is G.I.F.)
Ais continuous on $(0, \frac{π}{2})$
Bis strictly increasing in $(0, \frac{π}{2})$
Cis strictly decreasing in $(0, \frac{π}{2})$
Dhas global maximum value 2
The function $f (x) = \frac{1 - sin x + cos x}{1 + sin x + cos x}$ is not defined at $x = π$ . The value of $f (π)$ , so that f(x) is continuous at $x = π$ is
A $\frac{1}{2}$
B $\frac{1}{2}$
C $- 1$
D1
The function $f (x) = {tan}^{- 1} (sin x + cos x)$ is an increasing function in
A $(0, \frac{π}{2})$
B $- (\frac{π}{2}, \frac{π}{2})$
C $(\frac{π}{4}, \frac{π}{2})$
D $- (\frac{π}{2}, \frac{π}{4})$

IIT JEE PREVIOUS YEAR-LIMIT,CONTINUITY AND DIFFERENTIABILITY -Differentiability at a point ( Objective Questions II)

Home
Ask Doubt
Profile