Doubtnut Promotions Sticky

Let h(x)=min{x,x2}, for every real number of X. Then (A) h is continuous for all x (B) h is differentiable for all x (C) h′(x) = 1, for all x > 1 (D) h is not differentiable at two values of x

A

h is continuous for all x

B

h is differentiable for all x

C

h'(x)=1,∀x>1

D

h is not differentiable at two values of x

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, C, D

From the figure,
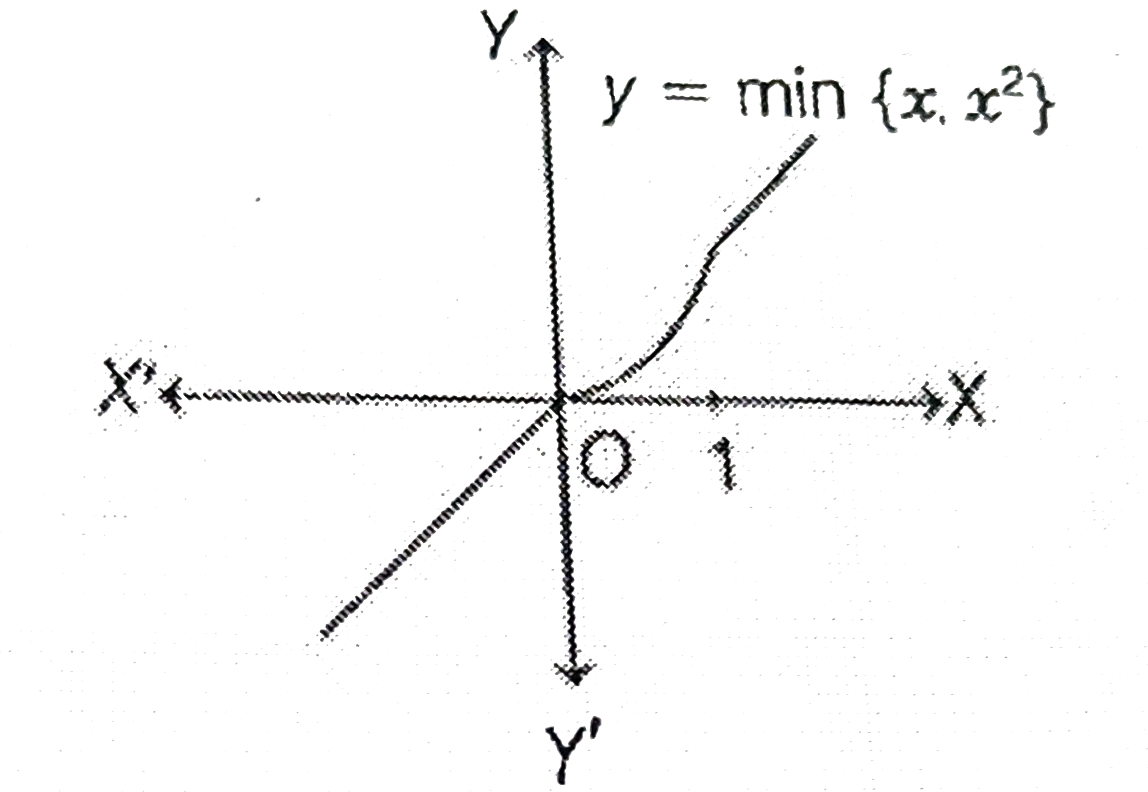
ocr_image
h(x) is continuous all x, but h(x) is not differentiable at two points x = 0 and x = 1 . (due to sharp edges). Also h'(x)=1,∀x>1.
Hence, (a) , (c ) and (d) is correct answers.

|
Updated on:21/07/2023
Class 12MATHSLIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let h(x) = Min. (x,x2), for every real number x, then

    Ah is discountious for all x
    Bh is differentiable for all x
    Ch(x) = 2, for all x<1
    Dh is not differentiable at two value of x
  • Question 2 - Select One or More

    Let h(x)=f(x)−(f(x))2+(f(x))3 for every real number x: Then

    Ah is increasing whenever f is increasing
    Bh is increasing whenever f is decreasing
    Ch is decreasing whenever f is decreasing
    Dnothing can be said in general.
  • Question 3 - Select One

    Let f be differentiable for all x. If f(1)=-2 and f'(x)≥2 for all x∈[1,6], then the minimum value of f(6) is

    A4
    B2
    C8
    DNone of these