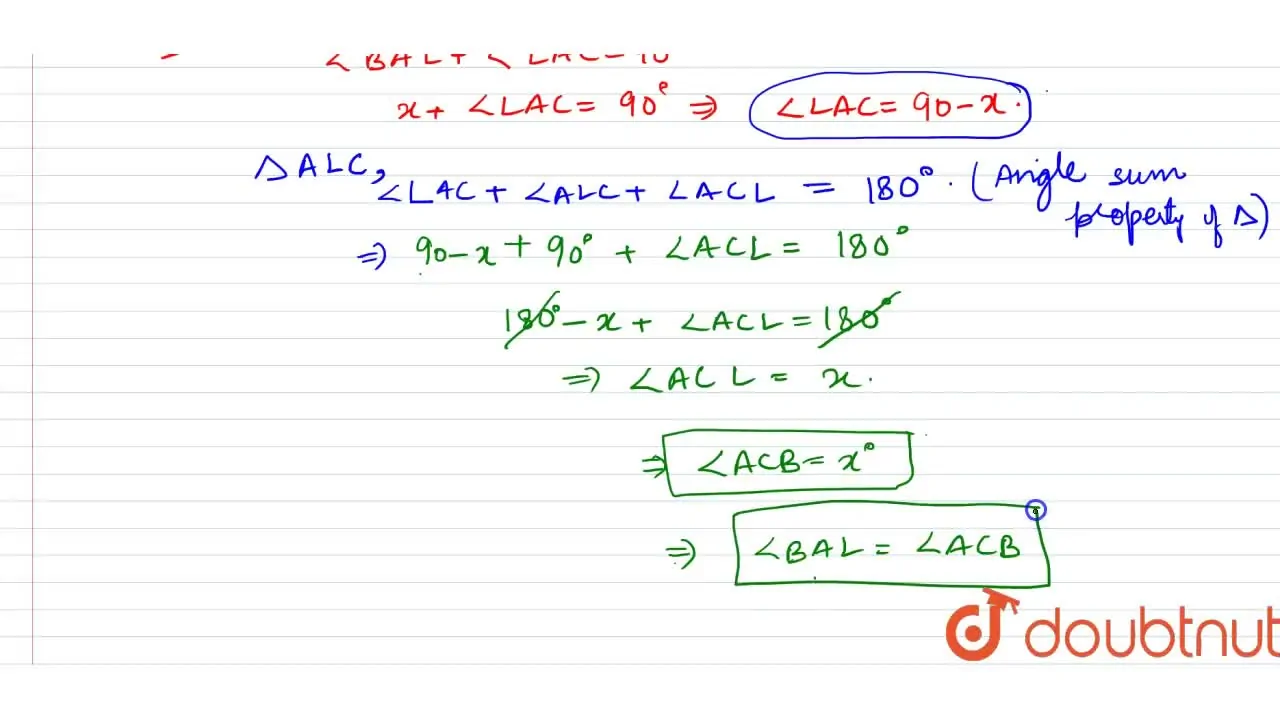
A Δ ABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
Given In ΔABC,∠A=90∘ and AL ⊥BC
To prove ∠BAL=∠ACB
Proof In ΔABCandΔLAC, ∠BAC=∠ALC [each90∘]…..(i)
and ∠ABC=∠ABL [common angle] ....(ii)

On adding Eqs. (i) and (ii), we get ∠BAC+∠ABC+∠ALC+∠ABL .....(iii)
Again, in ΔABC,∠BAC+∠ACB+∠ABC=180∘ .....(iv)
[sum of all angles of a triangles is 180∘]
⇒INΔABC,∠ABL+∠ALB+∠BAL180∘ [sum of all angles of a triangle is 180∘]
⇒ ∠ABL+∠ALC=180∘∠BAL [∴∠ALC=∠ALB=90∘] ...(V)
On substituting the value from Eqs. (iv) and (v) in Eq. (iii), we get
180∘−∠ACB=180∘−∠BAL
⇒ ∠ACB=∠BAL
Hence proved.
Related Playlists
Similar Questions
A triangle ABC is right angled at A.AL is drawn perpendicular to BC . Prove that ∠BAL=∠ACB.
View SolutionA triangle ABC is right angled at A. AL is drawn perpendicular to BC. Prove that ∠BAL=∠ACB
View SolutionA triangle ABC is right angles at A.AL is drawn perpendicular to BC . Prove that ∠BAL= ∠ACB
View SolutionIf ABC is an equilateral triangle and D is a point on BC such that AD⊥BC, then
View SolutionΔABC is right angled at A and AD⊥BC. Then BDDC=
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn a right tringle ABC, right-angled at B, D is a point on hypotenuse such that BD⊥AC. If DP⊥ABandDQ⊥BC then prove that
(a)DQ2=DP⋅QC DP2=DQ⋅AP.
 View Solution
View SolutionABC is a triangle right- angled at B and D is a point on BC produced (BD>BC), such that BD=2DC. Which one of the following is correct?
View SolutionABC is a triangle right-angled at B and D is a point on BC produced (BD > BC), such that BD = 2 DC. Which one of the following is correct?
View SolutionTriangle ABC is right angle at A. The points P and Q are on hypotenuse BC such that BP=PQ=QC.if AP=3andAQ=4, then length BC is equal to
View Solution