AB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
TO prove= PXQY is a recctangle
Proof-
AB||CD
∠AXY=∠DYX
12∠AXY=12∠DYX
∠1=∠2
XY intersect PX and QY at XY
∠1=∠2
PX||QY
Since,AB||CD and XY is transverse
∠BXY+∠OYX=180∘
2∠3+2∠2=180
∠3+∠2=90∘
In ∠XQY
∠2+∠3+∠XBY=180∘
90∘+∠XQY=180∘
∠XBY=90∘
∠XPY=∠XQY=∠PYQ=∠QXP=90∘
PXQY is a rectangle.
Related Playlists
Similar Questions
AB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View SolutionAB and CD are two parallel lines and a transversal 'l' intersects these lines at X and Y respectively Prove that the bisectors of interior angles from a parallelogram whose each angle is 90∘.
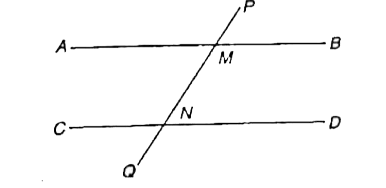
View SolutionAB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :
 View Solution
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionA transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
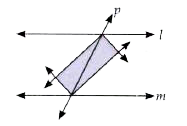
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
 View Solution
View Solution


