If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
To prove that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle, follow these steps:
Step 1: Understand the Setup
Let lines l1 and l2 be two parallel lines, and let t be a transversal that intersects l1 and l2. Label the angles formed at the intersections. Let the angles on line l1 be a and b, and the corresponding angles on line l2 be c and d.
Hint: Identify the angles formed by the transversal with the parallel lines and label them clearly.
Step 2: Use the Property of Parallel Lines
Since l1 and l2 are parallel, we know that:
- a+b=180∘ (co-interior angles)
- c+d=180∘ (co-interior angles)
Hint: Recall that the sum of the interior angles on the same side of the transversal is 180 degrees.
Step 3: Find the Angle Bisectors
Let the angle bisector of angle a be m and the angle bisector of angle b be n. Similarly, let the angle bisector of angle c be p and the angle bisector of angle d be q.
Hint: Remember that the angle bisector divides an angle into two equal parts.
Step 4: Calculate the Angles of the Bisectors
The angle bisectors will create the following angles:
- Angle m=a2
- Angle n=b2
- Angle p=c2
- Angle q=d2
Since a+b=180∘, we have:
- m+n=a2+b2=a+b2=180∘2=90∘
Similarly, for the angles on line l2:
- p+q=c2+d2=c+d2=180∘2=90∘
Hint: Use the property of angle bisectors to find the measures of the angles formed.
Step 5: Show that the Bisectors are Perpendicular
From the calculations above, we have:
- m+n=90∘
- p+q=90∘
This means that the angle formed between the bisectors m and p is 90∘ and the angle formed between the bisectors n and q is also 90∘.
Hint: Recognize that if two angles add up to 90 degrees, they are perpendicular.
Step 6: Conclude that the Bisectors Enclose a Rectangle
Since the angle bisectors m and p are perpendicular to each other and the angle bisectors n and q are also perpendicular to each other, the figure formed by these bisectors is a rectangle.
Hint: Recall that a rectangle is defined as a quadrilateral with four right angles.
Final Conclusion
Thus, we have proved that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle.
---
Let lines l1 and l2 be two parallel lines, and let t be a transversal that intersects l1 and l2. Label the angles formed at the intersections. Let the angles on line l1 be a and b, and the corresponding angles on line l2 be c and d.
Since l1 and l2 are parallel, we know that:
- a+b=180∘ (co-interior angles)
- c+d=180∘ (co-interior angles)
Let the angle bisector of angle a be m and the angle bisector of angle b be n. Similarly, let the angle bisector of angle c be p and the angle bisector of angle d be q.
The angle bisectors will create the following angles:
- Angle m=a2
- Angle n=b2
- Angle p=c2
- Angle q=d2
- m+n=a2+b2=a+b2=180∘2=90∘
- p+q=c2+d2=c+d2=180∘2=90∘
From the calculations above, we have:
- m+n=90∘
- p+q=90∘
Since the angle bisectors m and p are perpendicular to each other and the angle bisectors n and q are also perpendicular to each other, the figure formed by these bisectors is a rectangle.
Thus, we have proved that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle.
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example
13 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
Knowledge Check
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
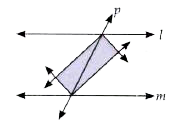 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquareIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
A1B2C3D4
If two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
