Water is filled to a height in a long container. From what height below the free surface a hole should be bored in the wall of a container so that the horizontal range is maximum?
Let h is the height of the hole below the free surface of water.
If H = total height of water
Then H -h= height of hole from ground
u= horizontal velocity of water coming out from hole =√2gh
t=time taken by water to cover vertical distance (H-h) before reaching the ground
(H−h)=12>2
t=√2(H−h)g
Horizontal range =R=ut
=(√2gh)√2(H−h)g
R=√4h(H−h)=2√hH−h2
Horizontal range in maximum if dRdh=0
dRdh=2×12(hH−h2)−12(H−2h)=0
Solving we get H=2h or h=H/2
Hole should be made hiddle of the initial water level in container.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Knowledge Check
- Question 1 - Select One
Water is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
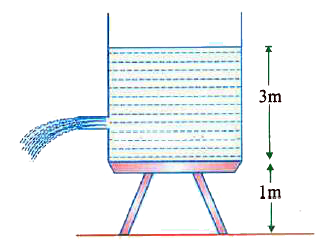 A3 m from groundB1 m from groundC4 m from groundD2 m from ground
A3 m from groundB1 m from groundC4 m from groundD2 m from ground - Question 1 - Select One
A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h - Question 1 - Select One
Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
A(a) 50B(b) 51C(c) 48D(d) 51.5 - Question 1 - Select One
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDg - Question 1 - Select One
The diagram shows a tall cylindrical container kept on a horizontal surface. From a tap, water come with constant rate qm3/s. Initially the container was empty. An orifice of area of cross section A is made at some height h in the side wall of the container. If the horizontal range of the water jet in steady is found to be 2h, then the relation between h and q is
 Ah=q2gA2Bh=q22gA2Ch=3q22gA2Dh=2q2gA2
Ah=q2gA2Bh=q22gA2Ch=3q22gA2Dh=2q2gA2
Similar Questions
Water is filled to a height of 2.5m in a container lying rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side √3 and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than 4×104 pascal
a, What minimum acceleration can be given to the container in the positive x-direction so that the cap will come out of the hole? Assume water does not spill out of container when the container accelerates.
Find the velocity of efflux as soon as the container starts moving with the acceleration calculated in part a. of the question.
 View Solution
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
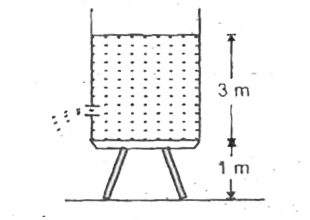 View Solution
View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
 View Solution
View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View Solution

