Water is filled to a height in a long container. From what height below the free surface a hole should be bored in the wall of a container so that the horizontal range is maximum?
To solve the problem of determining the height below the free surface from which a hole should be bored in a container filled with water to maximize the horizontal range of the water jet, we can follow these steps:
Step 1: Define the Variables
Let:
- H = height of water in the container from the bottom to the free surface.
- h = height below the free surface where the hole is bored.
- Therefore, the height from the bottom of the container to the hole is H−h.
Step 2: Determine the Velocity of the Water Jet
Using Torricelli's theorem, the velocity U of the water jet exiting the hole can be expressed as:
U=√2g(H−h)
where g is the acceleration due to gravity.
Step 3: Calculate the Time of Flight
The time T for the water jet to fall from the height H−h to the ground can be calculated using the formula for free fall:
T=√2(H−h)g
Step 4: Determine the Horizontal Range
The horizontal range R of the water jet can be calculated as:
R=U⋅T
Substituting the expressions for U and T:
R=√2g(H−h)⋅√2(H−h)g=2(H−h)
Step 5: Maximize the Range
To maximize the range R, we need to find the value of h that maximizes R=2(H−h).
Step 6: Differentiate and Set to Zero
Differentiate R with respect to h:
dRdh=−2
Setting the derivative equal to zero does not yield a maximum since it is a constant. Instead, we can analyze the function R directly.
Step 7: Analyze the Range Function
The range R=2(H−h) is a linear function that decreases as h increases. Therefore, to maximize R, we need to minimize h. The maximum range occurs when h is at its minimum value.
Step 8: Conclusion
To achieve maximum horizontal range, the hole should be bored at a height h equal to H2 below the free surface. Hence, the optimal height below the free surface is:
h=H2
Let:
- H = height of water in the container from the bottom to the free surface.
- h = height below the free surface where the hole is bored.
- Therefore, the height from the bottom of the container to the hole is H−h.
Using Torricelli's theorem, the velocity U of the water jet exiting the hole can be expressed as:
U=√2g(H−h)
where g is the acceleration due to gravity.
The time T for the water jet to fall from the height H−h to the ground can be calculated using the formula for free fall:
T=√2(H−h)g
The horizontal range R of the water jet can be calculated as:
R=U⋅T
Substituting the expressions for U and T:
R=√2g(H−h)⋅√2(H−h)g=2(H−h)
To maximize the range R, we need to find the value of h that maximizes R=2(H−h).
Differentiate R with respect to h:
dRdh=−2
Setting the derivative equal to zero does not yield a maximum since it is a constant. Instead, we can analyze the function R directly.
The range R=2(H−h) is a linear function that decreases as h increases. Therefore, to maximize R, we need to minimize h. The maximum range occurs when h is at its minimum value.
To achieve maximum horizontal range, the hole should be bored at a height h equal to H2 below the free surface. Hence, the optimal height below the free surface is:
h=H2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)
54 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)
3 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)
5 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Water is filled to a height of 2.5m in a container lying rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side √3 and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than 4×104 pascal
a, What minimum acceleration can be given to the container in the positive x-direction so that the cap will come out of the hole? Assume water does not spill out of container when the container accelerates.
Find the velocity of efflux as soon as the container starts moving with the acceleration calculated in part a. of the question.

View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
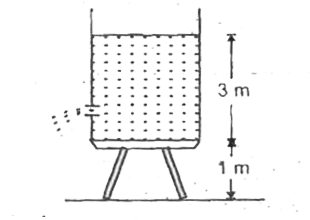
View Solution
Knowledge Check
Water is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
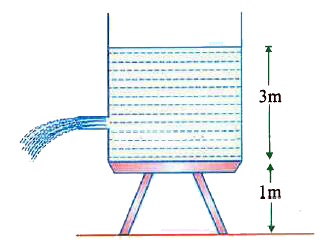 A3 m from groundB1 m from groundC4 m from groundD2 m from ground
A3 m from groundB1 m from groundC4 m from groundD2 m from groundA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
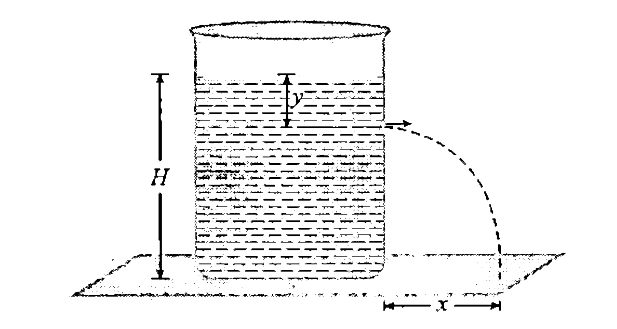 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−hWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
A(a) 50B(b) 51C(c) 48D(d) 51.5
Water level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionThe diagram shows a tall cylindrical container kept on a horizontal surface. From a tap, water come with constant rate qm3/s. Initially the container was empty. An orifice of area of cross section A is made at some height h in the side wall of the container. If the horizontal range of the water jet in steady is found to be 2h, then the relation between h and q is
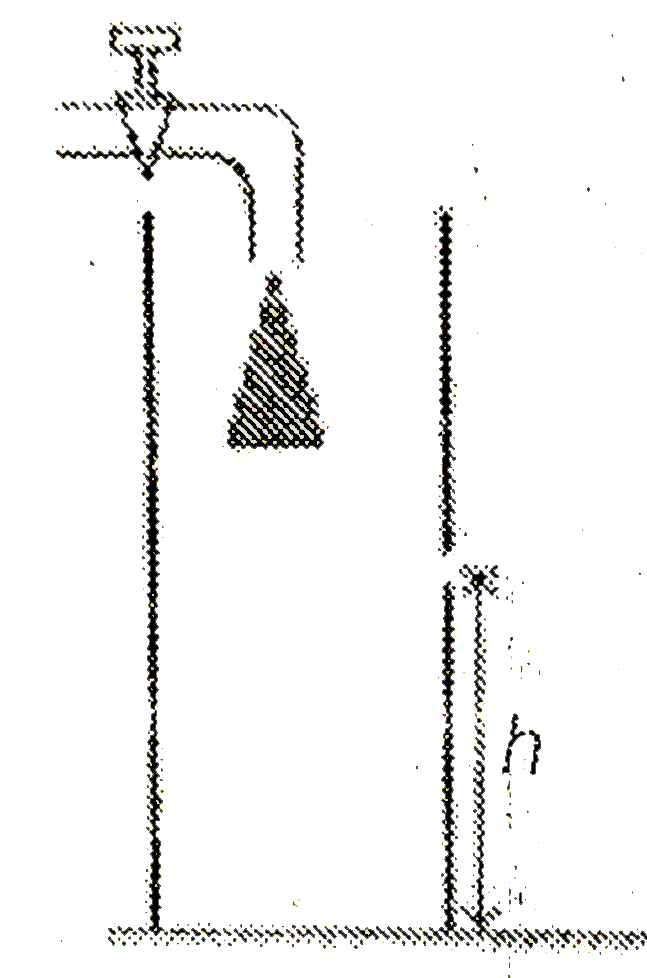
View Solution
