A wide cylindrical vessel $50 c m$ in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance $l_{max}$ from the vessel. Find $l_{max}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $25$

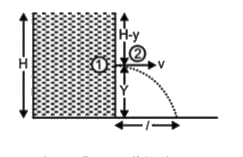
Applying Bernoulli.s theorem just inside (at point (1)) and just outside of the hole (at point (2))
$∴ \frac{P_{1}}{ρ g} + \frac{v_{1}^{2}}{2 g} + y = \frac{P_{2}}{ρ g} + \frac{v_{2}^{2}}{2 g} + y$
Here $v_{1} = 0, P_{2} = P_{0} =$ atmospheric pressure
$P_{1} = P_{0} + ρ g (H - y)$
$v_{2} = v$
Putting the values we obtain
$\frac{1}{2} ρ v^{2} = (H - y) ρ g$
$∴ v = \sqrt{2 g (H - y)}$
( in horizontal direction)
Horizontal range $I = v t$
For vertical motion
$y = \frac{1}{2} {gt}^{2}$
$∴ t = \sqrt{\frac{2 y}{g}}$
$∴ l = \sqrt{2 g (H - y)} \sqrt{\frac{2 y}{g}}$
$= 2 \sqrt{y (H - y)}$
For the maximum value of $l, \frac{d l}{d h} = 0$
After solving $y = \frac{H}{2} = 25 c m$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cylindrical vessel contains a liquid of density $ρ$ up to height $h$ . The liquid is closed by a piston of mass $m$ and area of cross section $A$ . There is a small hole at the bottom of the vessel. The speed $v$ with which the liquid comes out of the hole is

A $\sqrt{2 g h}$
B $\sqrt{2 (g h + \frac{m g}{p A})}$
C $\sqrt{2 (g h + \frac{m g}{A})}$
D $\sqrt{2 g h + \frac{m g}{A}}$
Question 2 - Select One
A cylindrical vessel contains a liquid of density $ρ$ up to height $h$ . The liquid is closed by a piston of mass $m$ and area of cross section $A$ . There is a small hole at the bottom of the vessel. The speed $v$ with which the liquid comes out of the hole is

A $\sqrt{2 g h}$
B $\sqrt{2 (g h + \frac{m g}{ρ A})}$
C $\sqrt{2 (g h + \frac{m g}{A})}$
D $\sqrt{2 (g h + \frac{m g}{A})}$
Question 3 - Select One
Figure shows a cylindrical vessel of height 90 cm filled upto the brim . There are four holes in the vessel as shows in figure . The liquid falling at maximum horizontal distance from the vessel would come from
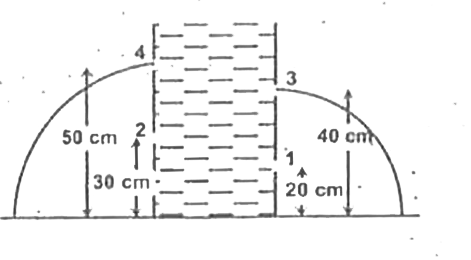Ahole 1
Bhole 2
Chole 3
Dhole 4

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 103-PHYSICS

Home
Ask Doubt
Profile