The two bodies of mass m1andm2(m1>m2) respectively are tied to the ends of a muscles string, which passes over a light and frictionless pulley. The masses are initially at rest and then released. Then acceleration of the centre of mass of the system is

(m1−m2m1+m2)2g
(m2−m1m1+m2)2g
m1gm1+m2
zero
The correct Answer is:A
In the pulley arrangement, |a1|=|a2|=a=[m1−m2m1+m2]g
but a1 is in downward direction and a2 in the upward direction, ie, a2=−a1.
∴ Acceleration of centre of mass
aCM=m1a1+m2a2m1+m2=m1m1+m2[m1−m2m1+m2]g−m2m1+m2[m1−m2m1+m2]g=(m1−m2m1+m2)2g
Similar Questions
Two bodies of masses m1 and m2(m1>m2) respectively are tied to the ends j of a string which passes over a light frictionless pulley. The masses are intitially at rest and released. What is the acceleration of the centre of mass ?
View SolutionTwo blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
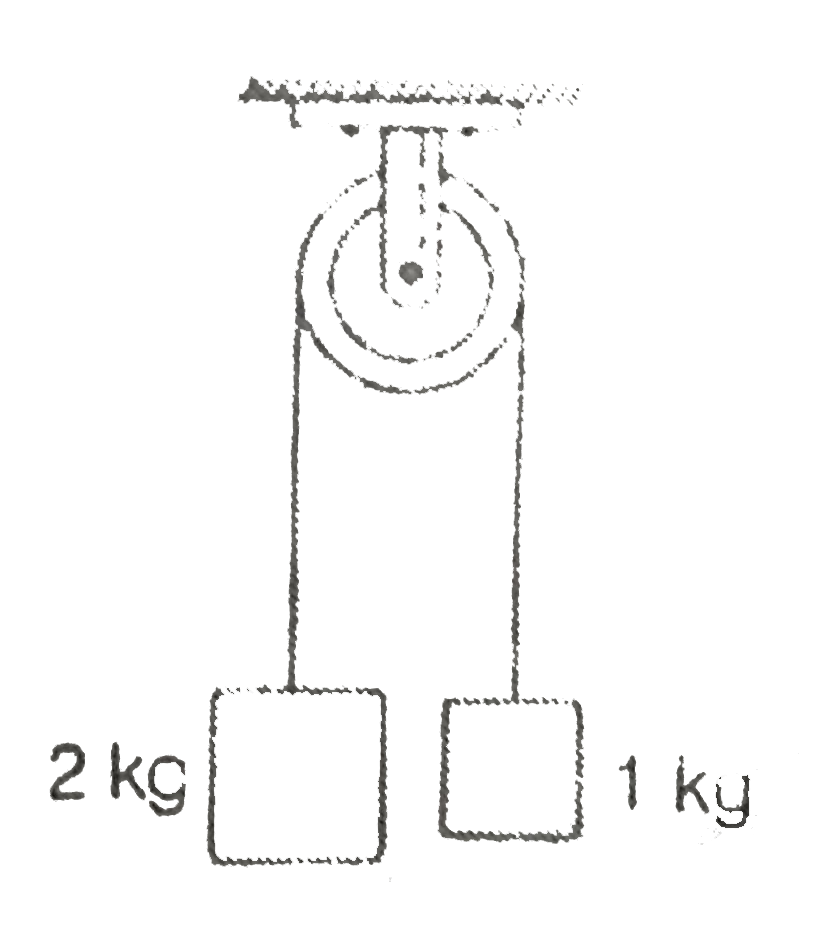 View Solution
View SolutionTwo blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
 View Solution
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
 View Solution
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
 View Solution
View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
View Solution

