The density (ρ) of an ideal gas varies with temperature T as shown in figure. Then

The correct Answer is:a=2t−2
a=t2−2t;
203m
a=2t−2
a. ∫v0dv=∫t0adt⇒v=(2t2/2t)t0=t2−2t
b. S=∫42vdt=(t33−2t22)42=203m.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Single Correct
Explore 52 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.4
Explore 16 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
The ednsity (ρ) of an ideal gas varies with temperature T as shown in figure. Then

View SolutionThe specific heat of an ideal gas varies with temperature T as
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure . The molar heat capacity of gas during this process is [R is gas constant]
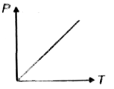
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
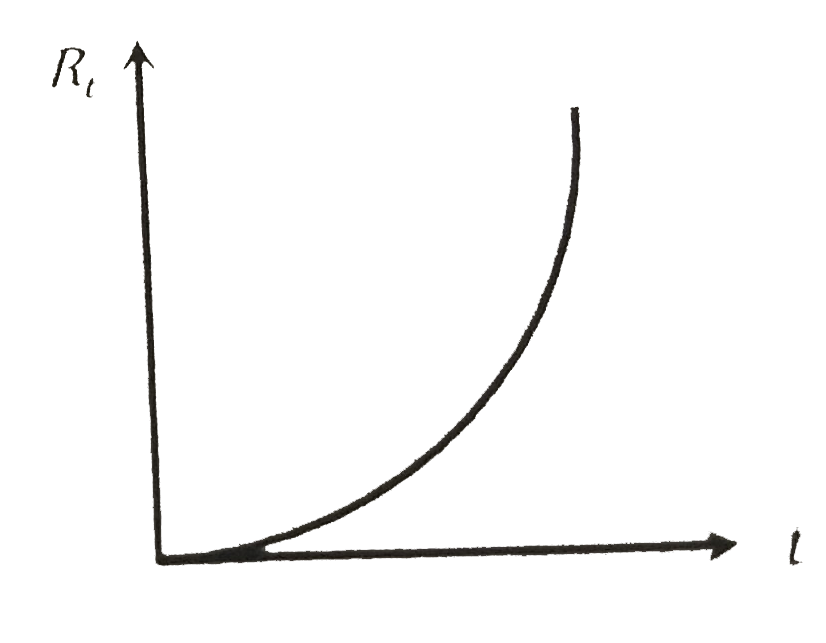
View Solutionthe volume( V) of a polyatomic( non linear molecule) gas varies with its temperature(T) , as shown in figure. The ratio of the heat absorbed by the gas to the work done by the gas, when gas is taken from state A to state B , is ( neglect vibrational mode)
_PHY_E05_037_Q01.png)
View SolutionIdeal gas is taken through the process shown in the figure :
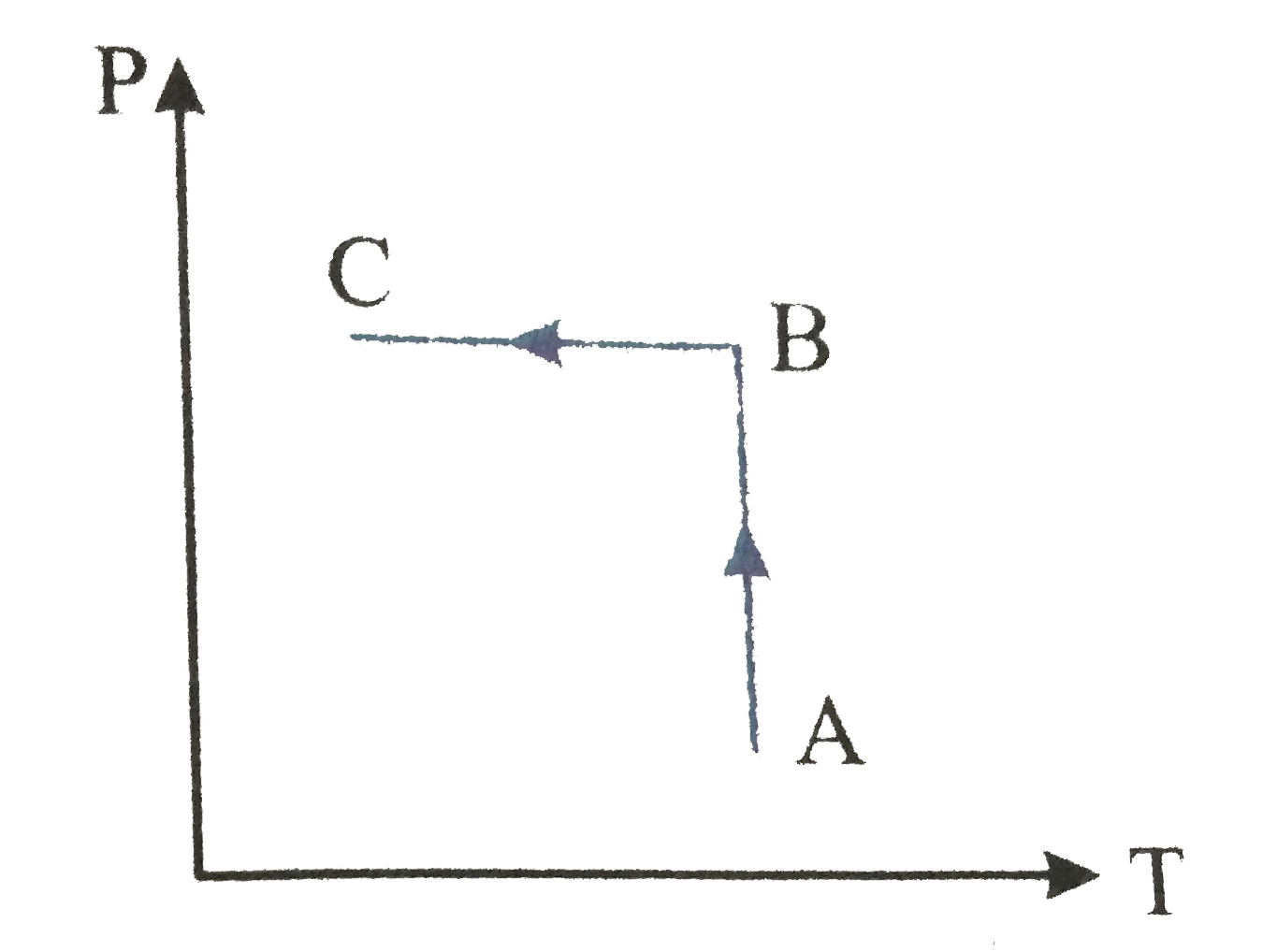
View SolutionIdeal gas is taken through the process shown in the figure :

View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionThe temperature of an ideal gas increases in an:
View SolutionThe graph of pressure and temperature for an ideal gas is as shown in figure. The given process is
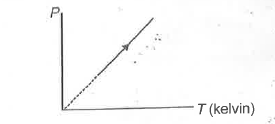
View Solution

