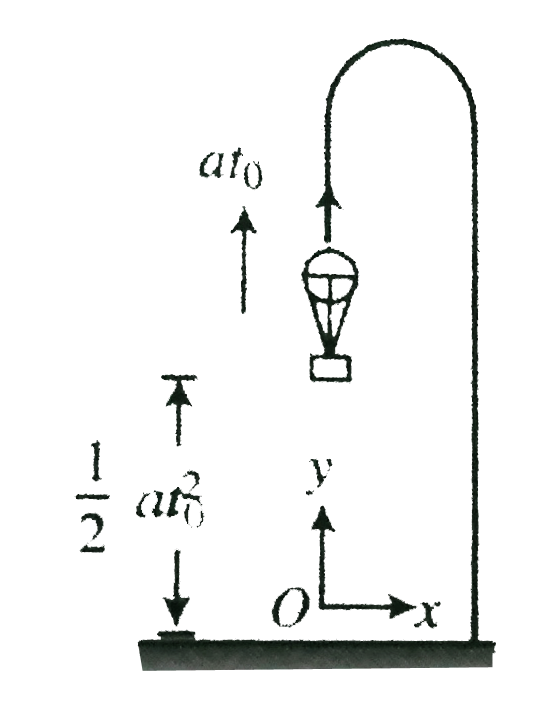
A ballon starts rising from ground from rest at some constant acceleration. After some time, a storne is dropped from it. If the stone reaches the ground in the same time in which balloon reached the dropping poing from ground, find the acceleration of the balloon.
The correct Answer is:g3
To solve the problem, we need to analyze the motion of the balloon and the stone separately. Let's break it down step by step.
Step 1: Define Variables
Let:
- a = acceleration of the balloon
- t0 = time taken for the balloon to reach the height where the stone is dropped
- g = acceleration due to gravity (approximately 9.81m/s2)
Step 2: Calculate the Velocity of the Balloon
The balloon starts from rest and accelerates upwards. The velocity of the balloon after time t0 can be calculated using the formula:
v=u+at
where u=0 (initial velocity). Thus:
v=0+at0=at0
Step 3: Calculate the Height of the Balloon
The height h reached by the balloon after time t0 can be calculated using the formula:
s=ut+12at2
Substituting u=0:
h=0+12at20=12at20
Step 4: Analyze the Motion of the Stone
When the stone is dropped from the balloon, it will take the same time t0 to reach the ground. The stone has an initial velocity equal to the velocity of the balloon at the moment of release, which is at0.
Using the second equation of motion for the stone:
s=ut+12gt2
Here, s is the height h (which is negative since it is falling), u=at0, and t=t0:
−h=at0t0+12gt20
Substituting h=12at20:
−12at20=at20+12gt20
Step 5: Rearranging the Equation
Rearranging the equation gives:
−12at20=at20+12gt20
−12at20−at20=12gt20
−32at20=12gt20
Step 6: Solve for a
Dividing both sides by 12t20:
−3a=g
Thus:
a=−g3
Since we are interested in the magnitude of acceleration:
a=g3
Final Answer
The acceleration of the balloon is:
g3
Let:
- a = acceleration of the balloon
- t0 = time taken for the balloon to reach the height where the stone is dropped
- g = acceleration due to gravity (approximately 9.81m/s2)
The balloon starts from rest and accelerates upwards. The velocity of the balloon after time t0 can be calculated using the formula:
v=u+at
where u=0 (initial velocity). Thus:
v=0+at0=at0
The height h reached by the balloon after time t0 can be calculated using the formula:
s=ut+12at2
Substituting u=0:
h=0+12at20=12at20
When the stone is dropped from the balloon, it will take the same time t0 to reach the ground. The stone has an initial velocity equal to the velocity of the balloon at the moment of release, which is at0.
s=ut+12gt2
Here, s is the height h (which is negative since it is falling), u=at0, and t=t0:
−h=at0t0+12gt20
Substituting h=12at20:
−12at20=at20+12gt20
Rearranging the equation gives:
−12at20=at20+12gt20
−12at20−at20=12gt20
−32at20=12gt20
Dividing both sides by 12t20:
−3a=g
Thus:
a=−g3
Since we are interested in the magnitude of acceleration:
a=g3
The acceleration of the balloon is:
g3
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Single Correct
52 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A balloon starts rising from ground from rest with an upward acceleration 2m/s2. Just after 1 s, a stone is dropped from it. The time taken by stone to strike the ground is nearly
View SolutionA stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
View SolutionA balloon starts rising from the ground with a constant acceleration of 1.25m/s2. After 8 s, a stone is released from the balloon. Find the time taken by the stone to reach the ground. (Take g=10m/s2)
View SolutionA balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
 .
.
View SolutionA stone dropped from a cliff hits the ground in 4 sec. Height of the cliff is
View SolutionA balloon rises from rest on the ground with constant acceleration g/8. A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA stone is dropped from the top of a tower. If it hits the ground after 10 seconds, what is the height of the tower?
View SolutionA balloon rises with uniform velocity of 10ms−1. When the balloon is at a height of 75 m if a stone is dropped from it the time taken by it to reach the ground is
View SolutionA balloon starts rising from the ground with an acceleration of 1.25 m/s2 . A stone is released from the balloon after 10s. Determine
(1) maximum height of ston from ground
(2) time taken by stone to reach the ground
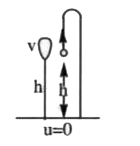
View SolutionA balloon starts from rest from the ground and moves with uniform acceleration g/8. When it reaches a height h a ball is dropped from it. Find the time taken by the ball to reach the ground.
View Solution
