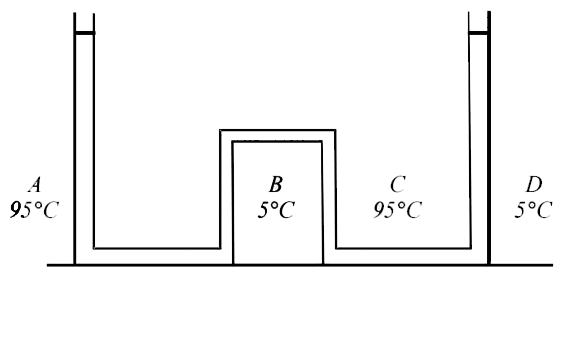
The apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of 95∘C while the columns B and D are maintained at 5∘C. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
The correct Answer is:γ=2×10−4/∘C
Density of a liquid varies with temperature as-
ρt∘c=(ρ0∘c1+γt)
Here γ is the coefficient of volume expansion of liquid.
 ltbr> In the figure-
ltbr> In the figure-
h1=52.8cm,h2=51cm and h=49cm
Now pressure at B=pressure at C
Therefore
P0+h1ρ95∘g−hρ5∘g=P0+h2ρ5∘g−hρ95∘g
⇒ρ95∘(h1+h)=ρ5∘(h2+h)
⇒ρ95∘ρ5∘=h2+hh1+h
⇒ρ0∘(1+95γ)ρ0∘(1+5γ)=h2+hh1+h
⇒1+5γ1+95γ=51+4952.8+49=100101.8
Solving this equaiton, we get
γ=2×10−4per.∘C
Topper's Solved these Questions
Similar Questions
Will the height of the water column change if the cross section of the water column is made wider ?
View Solution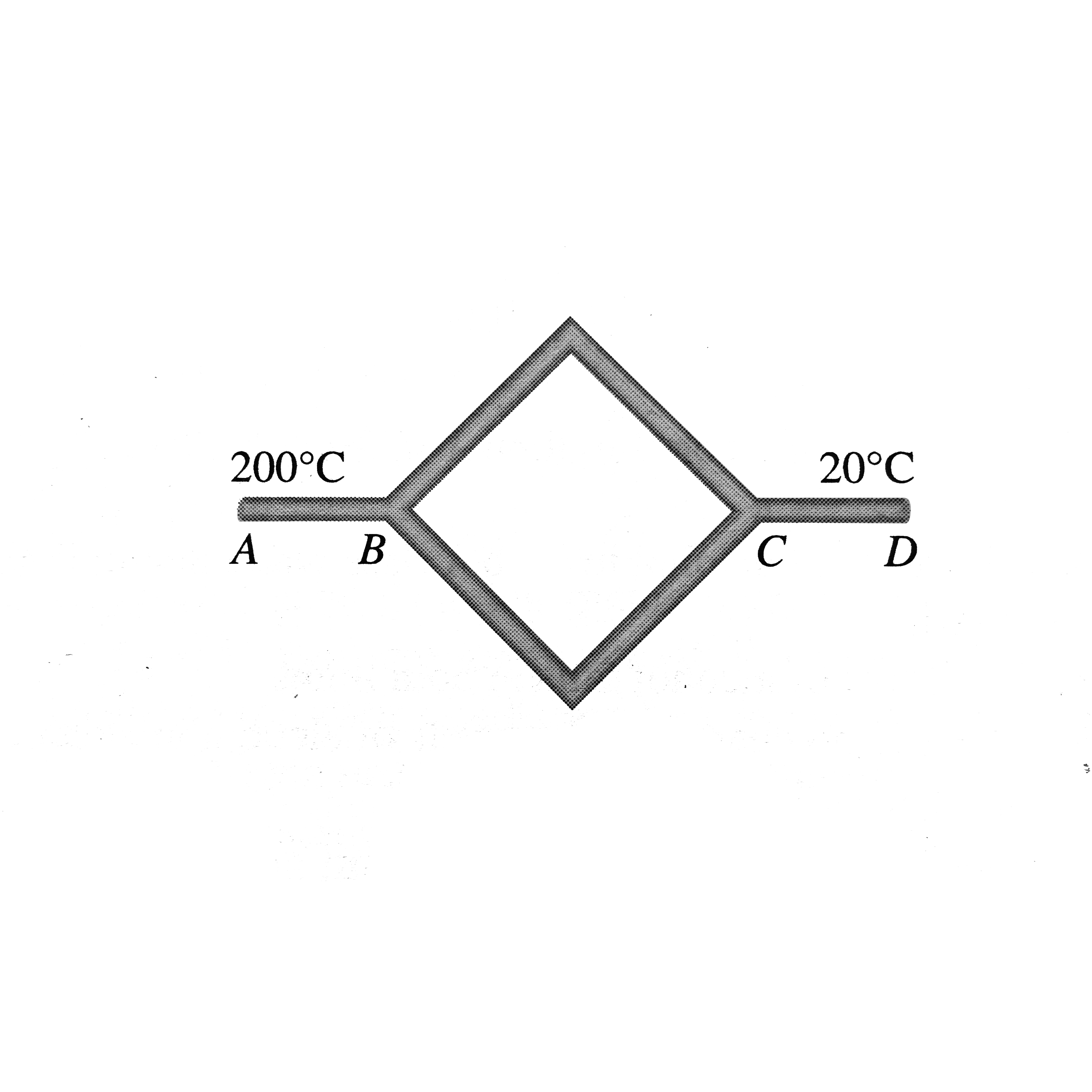
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView SolutionA vertical column 50 cm long at 50∘C balances another column of same liquid 60 cm long at 100∘C . The coefficient of absolute expansion of the liquid is
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
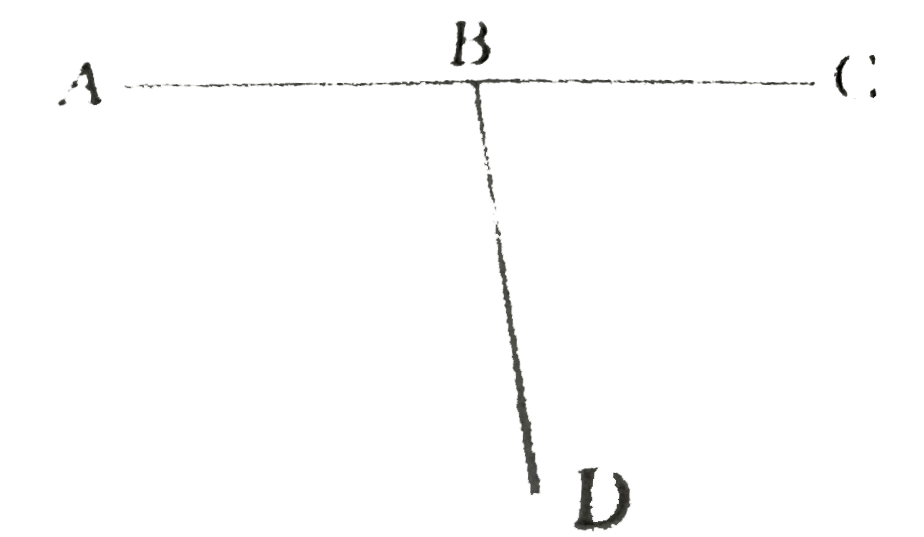
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20∘C,90∘Cand0∘C. The ratio of lengths BD and BC if there is no heat flow in AB is
 View Solution
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
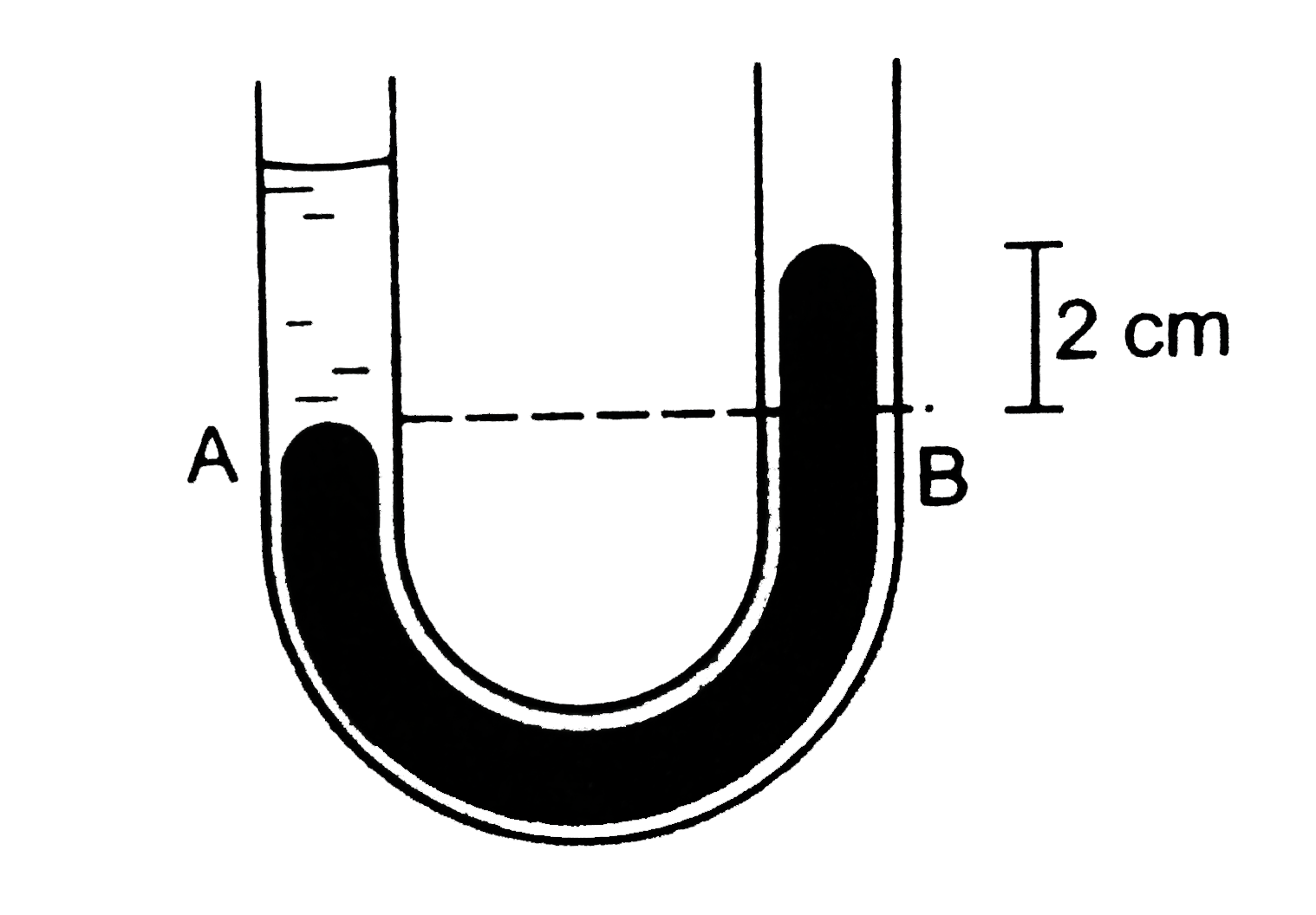 ,View Solution
,View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
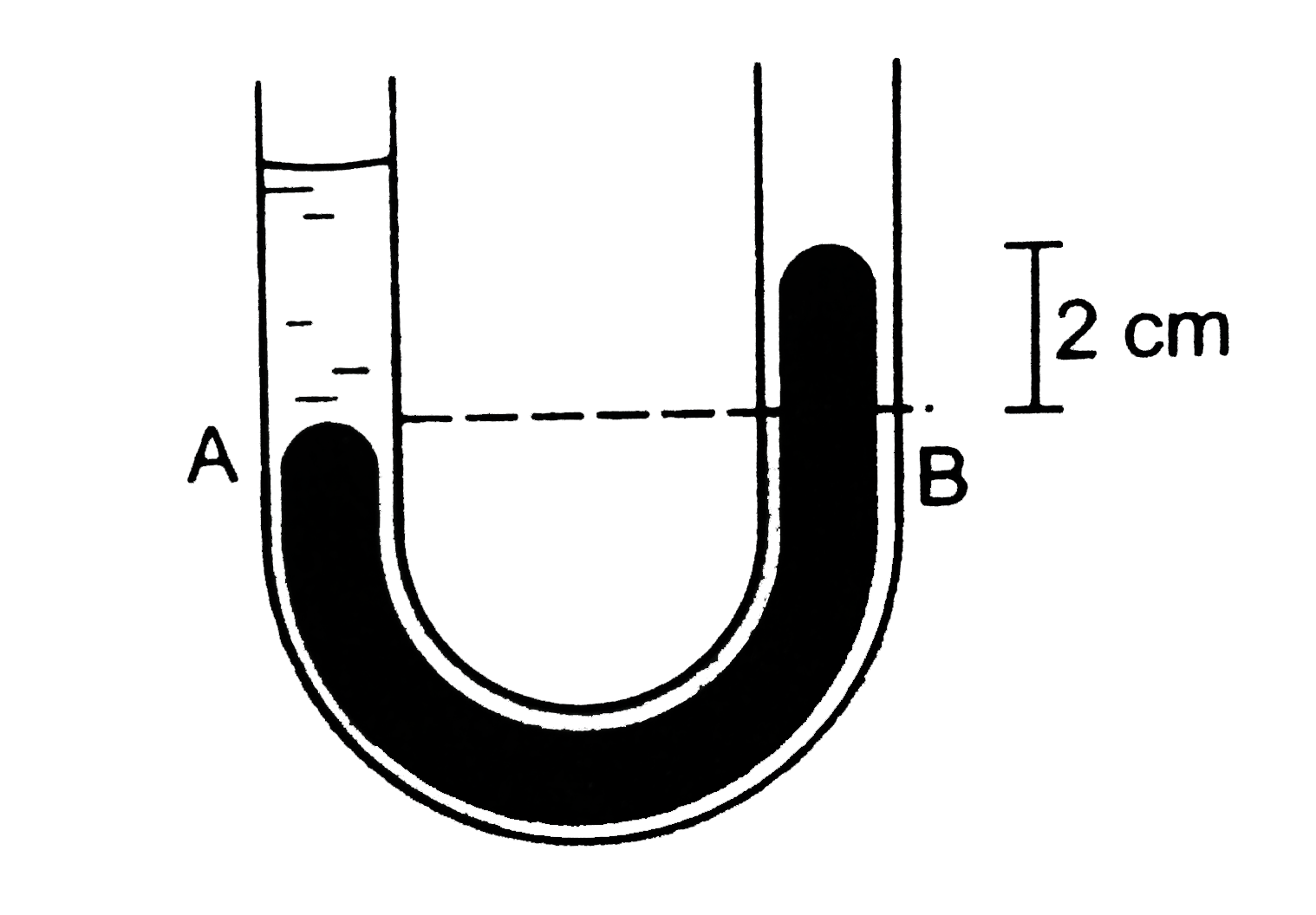 ,View Solution
,View Solution
