A vertical column 50 cm long at 50∘C balances another column of same liquid 60 cm long at 100∘C . The coefficient of absolute expansion of the liquid is
To find the coefficient of absolute expansion of the liquid, we can follow these steps:
Step 1: Understand the problem
We have two columns of the same liquid, one measuring 50 cm at 50°C and the other measuring 60 cm at 100°C. Since they balance each other, we can equate their volumes.
Step 2: Set up the equation for linear expansion
The linear expansion of a liquid can be described by the formula:
ΔL=L0⋅α⋅Δθ
where:
- ΔL is the change in length,
- L0 is the original length,
- α is the coefficient of linear expansion,
- Δθ is the change in temperature.
Step 3: Calculate the change in length and temperature
From the problem, we have:
- Length at 50°C, L1=50cm
- Length at 100°C, L2=60cm
- Change in length, ΔL=L2−L1=60cm−50cm=10cm
- Change in temperature, Δθ=100°C−50°C=50°C
Step 4: Substitute values into the linear expansion formula
We can use the length at 50°C as L0:
10cm=50cm⋅α⋅50°C
Step 5: Solve for α
Rearranging the equation gives:
α=10cm50cm⋅50°C
α=102500=1250cm−1⋅°C−1
Step 6: Convert to volumetric expansion
The coefficient of volumetric expansion (β) for liquids is approximately three times the coefficient of linear expansion:
β=3α=3⋅1250=3250=0.012°C−1=1.2×10−2°C−1
Final Answer
The coefficient of absolute expansion of the liquid is:
β=1.2×10−2°C−1
---
We have two columns of the same liquid, one measuring 50 cm at 50°C and the other measuring 60 cm at 100°C. Since they balance each other, we can equate their volumes.
The linear expansion of a liquid can be described by the formula:
ΔL=L0⋅α⋅Δθ
where:
- ΔL is the change in length,
- L0 is the original length,
- α is the coefficient of linear expansion,
- Δθ is the change in temperature.
From the problem, we have:
- Length at 50°C, L1=50cm
- Length at 100°C, L2=60cm
- Change in length, ΔL=L2−L1=60cm−50cm=10cm
- Change in temperature, Δθ=100°C−50°C=50°C
We can use the length at 50°C as L0:
10cm=50cm⋅α⋅50°C
Rearranging the equation gives:
α=10cm50cm⋅50°C
α=102500=1250cm−1⋅°C−1
The coefficient of volumetric expansion (β) for liquids is approximately three times the coefficient of linear expansion:
β=3α=3⋅1250=3250=0.012°C−1=1.2×10−2°C−1
The coefficient of absolute expansion of the liquid is:
β=1.2×10−2°C−1
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Try Youself16videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-A) Objective Type questions (one option is correct)50videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST2EXERCISE - EXERCISE2videos
TEST2
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)10videos
THERMODYNAMICS
Similar Questions
An aluminium measuring rod, which is correct at 5∘C measures the length of a line as 80 cm at 45∘C If thermal coefficient of linear expansion of aluminium is 2.50×10−4/∘C, the correct length of the line is:
View SolutionTwo vertical glass tibes filled with a liquid are connected at their lower ends by a horizontal capillary tube. One tube is surrounded by a bath containing ice and water at 0∘C and the other by hot water a t∘C. The difference in the height of the liquid in the two columns is Δh, and the height of the colume at 0∘C is h0. coefficient of volume expansion of the liquid is.
 View Solution
View SolutionA sphere of diameter 7.0 cm and mass 266.5 g float in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of 35∘C. If the density of liquid is 1.527gcm−3 at0∘C, find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere.
View SolutionA horizontal tube, open at both ends, contains a column of liquid. The length of this liquid column does not change with temperature. Let γ : coefficient of volume expansion of the liquid and α : coefficient of linear expansion of the material of the tube
View SolutionAn iron rod of length 50 cm is joined at an end to an aluminum rod of length 100 cm. All measurements refer to 20∘C . The coefficients of linear expansion of iron and aluminum are 12×10−6/∘Cand24×10−6/∘C, respectively. The average coefficient of expansion of composite system is :
View SolutionA metre rod of silver at 0∘C is heated to 100∘C. It's length is increased by 0.19 cm. coefficient of volume expansion of the silver rod is
View SolutionA sphere of diameter 7.0 cm and mass 266.5 g float in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of 350C. If the density of liquid is 1.527gcm−3 at 0oC, find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere.
View SolutionTwo vessels connected at the bottom by a thin pipe with a sliding plug contain liquid at 20∘C and 80∘C respectively. The coefficient of cubic expansion of liquid is 10−3K−1. The raio of height of liquid columns in the vessel (H20/H80) is nearest which interger ?
View SolutionTwo vessels connected at the bottom by a thin pipe with a sliding plug contain liquid at 20∘C and 80∘C respectively. The coefficient of cubic expansion of liquid is 10−3K−1. The ratio of height of liquid columns in the vessel (H20/H80) is nearest which integer ?
View Solution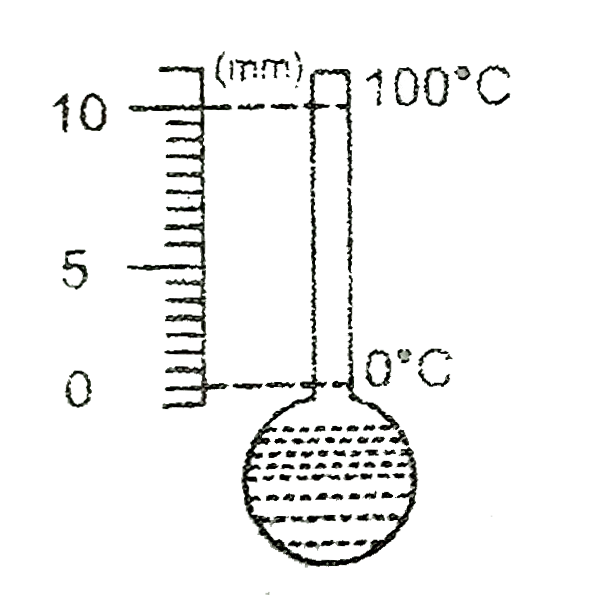
Level of a certain liquid at 0∘C and 100∘C are 0 and 10mm on a given fixed scale (as shown in fig.) coefficient of volume expansion this liquid varies with temperature as γ=γ0(1+T100) (where T in .∘C) Find the level (in mm) of liquid at 48∘CView Solution
