Two vessels connected at the bottom by a thin pipe with a sliding plug contain liquid at 20∘C and 80∘C respectively. The coefficient of cubic expansion of liquid is 10−3K−1. The raio of height of liquid columns in the vessel (H20/H80) is nearest which interger ?
To solve the problem, we need to find the ratio of the heights of the liquid columns in two vessels containing liquids at different temperatures. We will use the concept of pressure balance and the coefficient of cubic expansion.
1. Understanding the Setup:
We have two vessels connected at the bottom by a thin pipe. One vessel contains liquid at 20∘C and the other at 80∘C. The coefficient of cubic expansion of the liquid is given as γ=10−3K−1.
2. Establishing Pressure Balance:
Since the two vessels are connected, the pressure at the bottom of both vessels must be equal at the level of the connecting pipe. The pressure at a certain depth in a liquid is given by the formula:
P=ρgh
where P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
3. Setting up the Equation:
Let H20 be the height of the liquid column in the vessel at 20∘C and H80 be the height of the liquid column in the vessel at 80∘C. We can write the pressure balance as:
H20⋅ρ20⋅g=H80⋅ρ80⋅g
Here, g cancels out from both sides, leading to:
H20⋅ρ20=H80⋅ρ80
4. Expressing Densities:
The density of the liquid at different temperatures can be expressed using the coefficient of cubic expansion:
ρT=ρ0(1−γΔT)
where ΔT is the change in temperature from a reference temperature. For our case:
- For 20∘C: ΔT=20−20=0 so ρ20=ρ0
- For 80∘C: ΔT=80−20=60 so ρ80=ρ0(1−γ⋅60)
5. Calculating the Density at 80∘C:
Plugging in the values:
ρ80=ρ0(1−10−3⋅60)=ρ0(1−0.06)=ρ0⋅0.94
6. Substituting Densities into the Pressure Equation:
Now substituting ρ20 and ρ80 into our pressure balance equation:
H20⋅ρ0=H80⋅(0.94ρ0)
The ρ0 cancels out:
H20=0.94H80
7. Finding the Ratio:
Rearranging gives us the ratio of the heights:
H20H80=0.94
8. Rounding to the Nearest Integer:
The problem asks for the nearest integer to this ratio:
H20H80≈0.94≈1
Final Answer:
The ratio of the heights of the liquid columns H20/H80 is nearest to the integer 1.
We have two vessels connected at the bottom by a thin pipe. One vessel contains liquid at 20∘C and the other at 80∘C. The coefficient of cubic expansion of the liquid is given as γ=10−3K−1.
Since the two vessels are connected, the pressure at the bottom of both vessels must be equal at the level of the connecting pipe. The pressure at a certain depth in a liquid is given by the formula:
P=ρgh
where P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
Let H20 be the height of the liquid column in the vessel at 20∘C and H80 be the height of the liquid column in the vessel at 80∘C. We can write the pressure balance as:
H20⋅ρ20⋅g=H80⋅ρ80⋅g
Here, g cancels out from both sides, leading to:
H20⋅ρ20=H80⋅ρ80
The density of the liquid at different temperatures can be expressed using the coefficient of cubic expansion:
ρT=ρ0(1−γΔT)
where ΔT is the change in temperature from a reference temperature. For our case:
- For 20∘C: ΔT=20−20=0 so ρ20=ρ0
- For 80∘C: ΔT=80−20=60 so ρ80=ρ0(1−γ⋅60)
Plugging in the values:
ρ80=ρ0(1−10−3⋅60)=ρ0(1−0.06)=ρ0⋅0.94
Now substituting ρ20 and ρ80 into our pressure balance equation:
H20⋅ρ0=H80⋅(0.94ρ0)
The ρ0 cancels out:
H20=0.94H80
Rearranging gives us the ratio of the heights:
H20H80=0.94
The problem asks for the nearest integer to this ratio:
H20H80≈0.94≈1
The ratio of the heights of the liquid columns H20/H80 is nearest to the integer 1.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Two vessel connected by a pipe with a sliding plug contain mercury. In one vessel, the height of murcury column is 39.2cm and its temperature is 0∘C, while in the other, the height of mercury column is 40cm and its temperature is 100∘C. Find the coefficient if cubical expansion for mercury. The volume of the connecting pipe should be neglected.
View SolutionTwo liquids A and B boil at 130∘C and 160∘C , respectively. Which of the them has higher vapour pressure at 80∘C.
View SolutionTwo liquids A and B boil at 145∘C and 190∘C respectively. Which of them has a higher vapour pressure 80∘C?
View SolutionTwo liquids A and B boil at 130∘C and 160∘C , respectively. Which of the them has higher vapour pressure at 80∘C.
View SolutionTwo liquids at temperature 60∘C and 20∘C respectively have masses in the ratio 3:4 their specific heat in the ratio 4:5. If the two liquids are mixed, the resultant temperature is.
View SolutionConsider a cylindrical container of cross-section area A length h and having coefficient of linear expansion αc. The container is filled by liquid of real expansion coefficient γL up to height h1. When temperature of the system is increased by Δθ then
(a). Find out the height, area and volume of cylindrical container and new volume of liquid.
(b). Find the height of liquid level when expansion of container is neglected.
(c). Find the relation between γL and αc for which volume of container above the liquid level
(i) increases
(ii). decreases
(iii). remains constant.
(d). On the surface of a cylindrical container a scale is attached for the measurement of level of liquid of liquid filled inside it. If we increase the temperature of the temperature of the system by Δθ, then
(i). Find height of liquid level as shown by the scale on the vessel. Neglect expansion of liquid.
(ii). Find the height of liquid level as shown by the scale on the vessel. Neglect expansion of container.

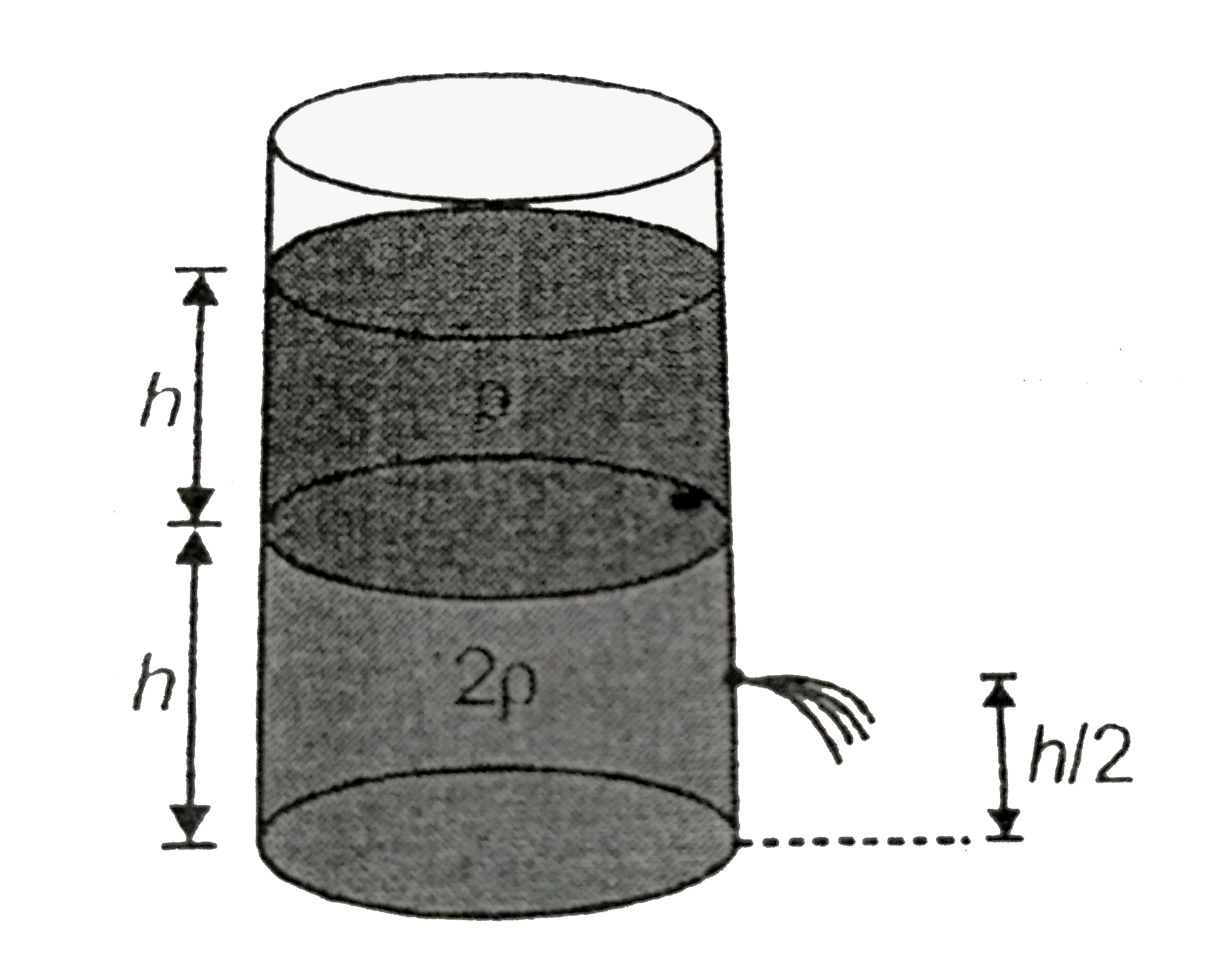
View SolutionA vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
View SolutionA metallic bob weights 50g in air. If it is immersed in a liquid at a temperature of 25∘C, it weights 45g . When the temperature of the liquid is raised to 100∘C, it weights 45.1g. Calculate the coefficient of cubical expansion of the liquid. Given that coefficient of cubical expansion of the metal is 12×10−6.∘C−1.
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View SolutionTwo vertical glass tibes filled with a liquid are connected at their lower ends by a horizontal capillary tube. One tube is surrounded by a bath containing ice and water at 0∘C and the other by hot water a t∘C. The difference in the height of the liquid in the two columns is Δh, and the height of the colume at 0∘C is h0. coefficient of volume expansion of the liquid is.

View Solution
