In two experiments with a countinous flow calorimeter to determine the specific heat capacity of a liquid,an input power of 16 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. Find the power lost (in W) to the surrounding in each case.
To solve the problem, we will analyze the two experiments with a continuous flow calorimeter and derive the power lost to the surroundings in each case.
1. Understanding the First Experiment:
- Given: Input power P1=16W
- Temperature rise ΔT=10K
- Let the power lost to the surroundings be q.
- The power gained by the liquid is given by the equation:
P1−q=dmdt⋅s⋅ΔT
- Rearranging gives us:
16−q=dmdt⋅s⋅10(Equation 1)
2. Understanding the Second Experiment:
- In this case, the input power is doubled: P2=32W.
- The flow rate of the liquid is three times faster, so the mass flow rate becomes 3⋅dmdt.
- The same temperature rise ΔT=10K is achieved.
- The power gained by the liquid in this case is:
P2−q=3⋅dmdt⋅s⋅ΔT
- Rearranging gives us:
32−q=3⋅dmdt⋅s⋅10(Equation 2)
3. Setting Up the Equations:
- We have two equations:
- From Experiment 1: 16−q=dmdt⋅s⋅10
- From Experiment 2: 32−q=3⋅dmdt⋅s⋅10
4. Dividing the Two Equations:
- Divide Equation 2 by Equation 1:
32−q16−q=3⋅dmdt⋅s⋅10dmdt⋅s⋅10
- This simplifies to:
32−q16−q=3
5. Cross-Multiplying:
- Cross-multiplying gives:
32−q=3(16−q)
- Expanding the right side:
32−q=48−3q
6. Solving for q:
- Rearranging gives:
3q−q=48−32
- This simplifies to:
2q=16
- Therefore:
q=8W
Conclusion:
The power lost to the surroundings in each case is 8W.
- Given: Input power P1=16W
- Temperature rise ΔT=10K
- Let the power lost to the surroundings be q.
- The power gained by the liquid is given by the equation:
P1−q=dmdt⋅s⋅ΔT
- Rearranging gives us:
16−q=dmdt⋅s⋅10(Equation 1)
- In this case, the input power is doubled: P2=32W.
- The flow rate of the liquid is three times faster, so the mass flow rate becomes 3⋅dmdt.
- The same temperature rise ΔT=10K is achieved.
- The power gained by the liquid in this case is:
P2−q=3⋅dmdt⋅s⋅ΔT
- Rearranging gives us:
32−q=3⋅dmdt⋅s⋅10(Equation 2)
- We have two equations:
- From Experiment 1: 16−q=dmdt⋅s⋅10
- From Experiment 2: 32−q=3⋅dmdt⋅s⋅10
- Divide Equation 2 by Equation 1:
32−q16−q=3⋅dmdt⋅s⋅10dmdt⋅s⋅10
- This simplifies to:
32−q16−q=3
- Cross-multiplying gives:
32−q=3(16−q)
- Expanding the right side:
32−q=48−3q
- Rearranging gives:
3q−q=48−32
- This simplifies to:
2q=16
- Therefore:
q=8W
The power lost to the surroundings in each case is 8W.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The temperature of a hot liquid in a container of negligible heat capacity falls at the rate of 3K/min due to heat emission to the surroundings, just before it begins to solidify. The temperature then remains constant for 30min, by the time the liquid has all solidfied. Find the ratio of specific heat capacity of liquid to specific latent heat of fusion.
View SolutionAn electric heater of power 1000 W raises the temperature of 5 kg of a liquid from 25∘C to 31∘C in 2 minutes. Calculate : (i) the heat capacity, and (ii) the specific heat capacity of liquid.
View SolutionA metal block of heat capacity 90J/.∘C placed in a room at 25∘C is heated electrically. The heater is switched off when the temperature reaches 35∘C. The temperature of the block rises at the rate of 2∘C/s just after the heater is switched on and falls at the rate of 0.2∘C/s just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is 30∘C. (d) Assuming that the power radiated at 30∘C respresents the average value in the heating process, find the time for which the heater was kept on.
View SolutionA dc motor works on the principle that a current carrying coil, when placed in a magnetic field experiences a torque. The arrangement consists of a coil suspended in a region of magnetic field. When a current is passed through the coil, it experiences torque and starts rotating. A simple arrangement is shown below.
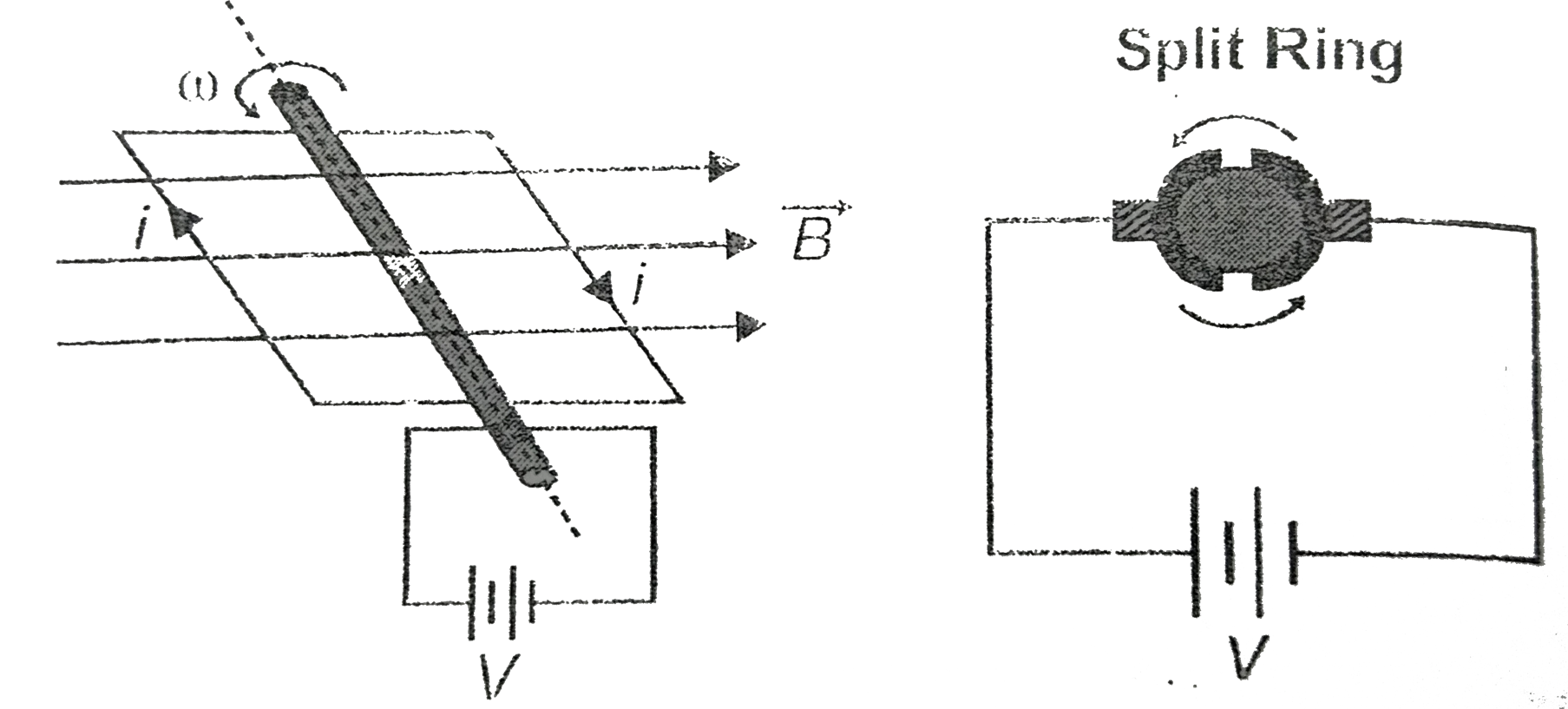
The coil rotates under the action of torque. The current is supplied to the coil by an arrangement of two sliding contacts and a split ring. As the coil rotates, the magnetic flux linked with the coil changes. This leads to production of an induced emf ε in the coil. By Lenz's law, the induced emf opposes the applied voltage and therefore, it is called back emf. If R is the resistance in the coil, the current i flowing through the coil at any instant is i=V−εR. The back emf is developed due to induction and it is directly proportional to speed of rotation and it is directly proportional to speed of rotation of the motor. There is a continuous power loss i2R in the motor, in form of heat.
When a dc motor is running unloaded (full speed) the current through it is 1 A. What will be the current flowing through the motor, when it is loaded to run at half its maximum speed, it applied voltage is 10 V and armature resistance is 5Ω
View SolutionThe reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be 2×10−3mol−1L and the rate constants for the formation of A2X and A2 in Step II and III are 3.0×10−2mol−1L−1min and 1×103mol−1L−1min (all data at 25∘C), then what is the overall rate constant (mol−2L2−1min) of the consumption of B2?
View SolutionThe reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
How many times the rate of formation of A2 will increase if concentrations of AX is doubled and that of B2 is increased theee fold?
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2
View SolutionWhen a block of metal of specific heat 0.1cal/g/∘C and weighing 110 g is heated to 100∘C and then quickly transferred to a calorimeter containing 200g of a liquid at 10∘C, the resulting temperature is 18∘C. On repeating the experiment with 400 g of same liquid in the same calorimeter at same initial temperature, the resulting temperature is 14.5∘C. find
a. Specific heat of the liquid.
b. The water equivalent of calorimeter.
View SolutionA heating coil is immersed in a calorimeter of heat capacity 50J∘C−1 containing 1.0 kg of a liquid of specific heat capacity 450 J kg−1∘C−1. The temperature of liquid rises by 10∘C when 2:0 A current is passed for 10 minutes. Find : (i) the resistance of the coil, (ii) the potential difference across the coil. State the assumption used in your calculations.
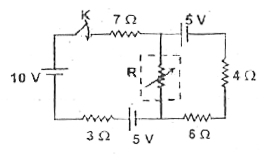
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View Solution
