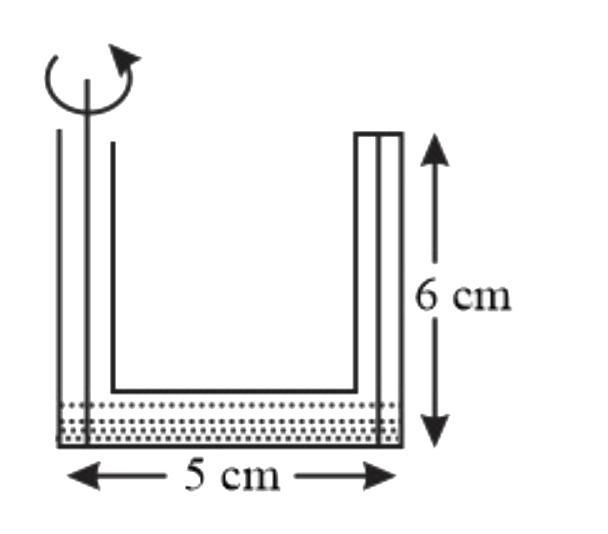
Length of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
The correct Answer is:100
Step by step video & image solution for Length of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of "7700 N m"^(-2). A liquid of density rho=10^(3)" kg m"^(-3) is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity omega due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of omega("in rad s"^(-1))? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Length of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)
 View Solution
View SolutionLength of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)
 View Solution
View SolutionA U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area=1cm2, It is filled with water of volume 60 cc. What volume of a liquid of density 4g/ should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube? a) 60 cc b) 45 cc c) 50 cc d) 35 cc
View SolutionA tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
View SolutionA liquid X of density 3.36g/cm3 poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
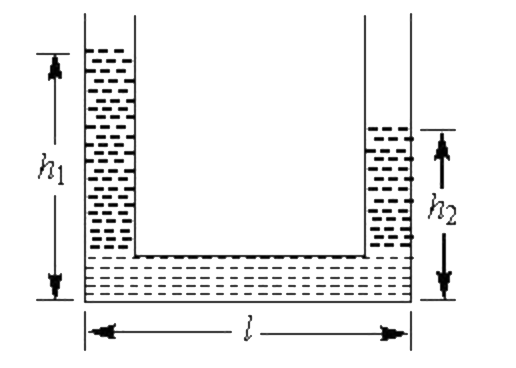
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
 View Solution
View SolutionA tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. Determine the force exerted by the liquid at the other end.
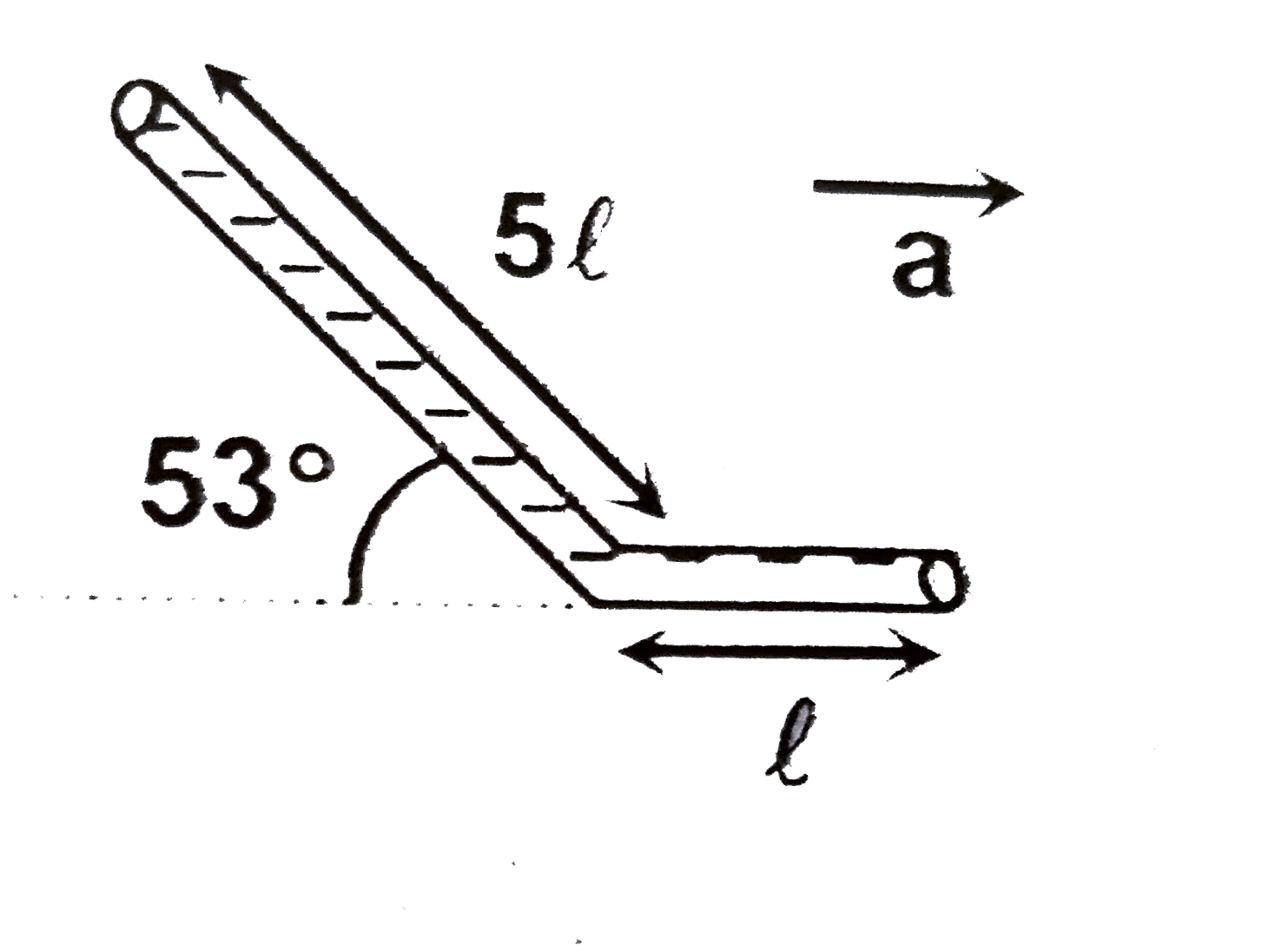
View SolutionIn the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.
 View Solution
View Solution_S01_015_Q01.png)
A vertical U-tube of uniform cross-section contains mercury in both arms A glycerine (relative density =1.3) column of length 10 cm is introduced into one of the arms. Oil of density 800 gm m−3 is poured into the other arm until the upper surface of the oil and hlycerine are at the same horizontal level, find the length of the column. Density of mercury is 13.6×103kgm−3View SolutionA U tube pf uniform born of cross sectional area A has been set up vertically with open ends facing up Now mgm of a liquid of density d is poured into it. The column of liquid in this tube will oscillation with a period T such that
View Solution


