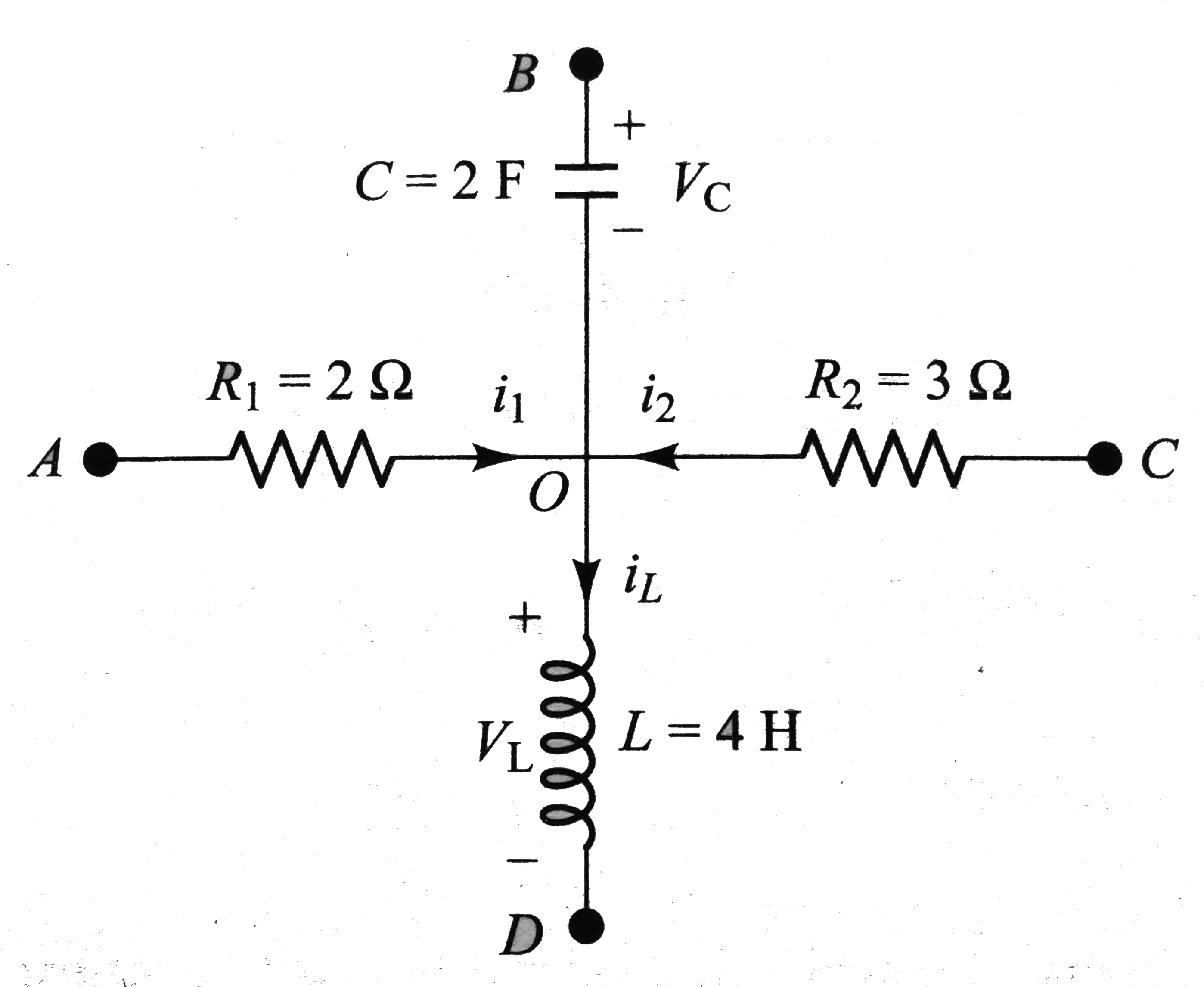
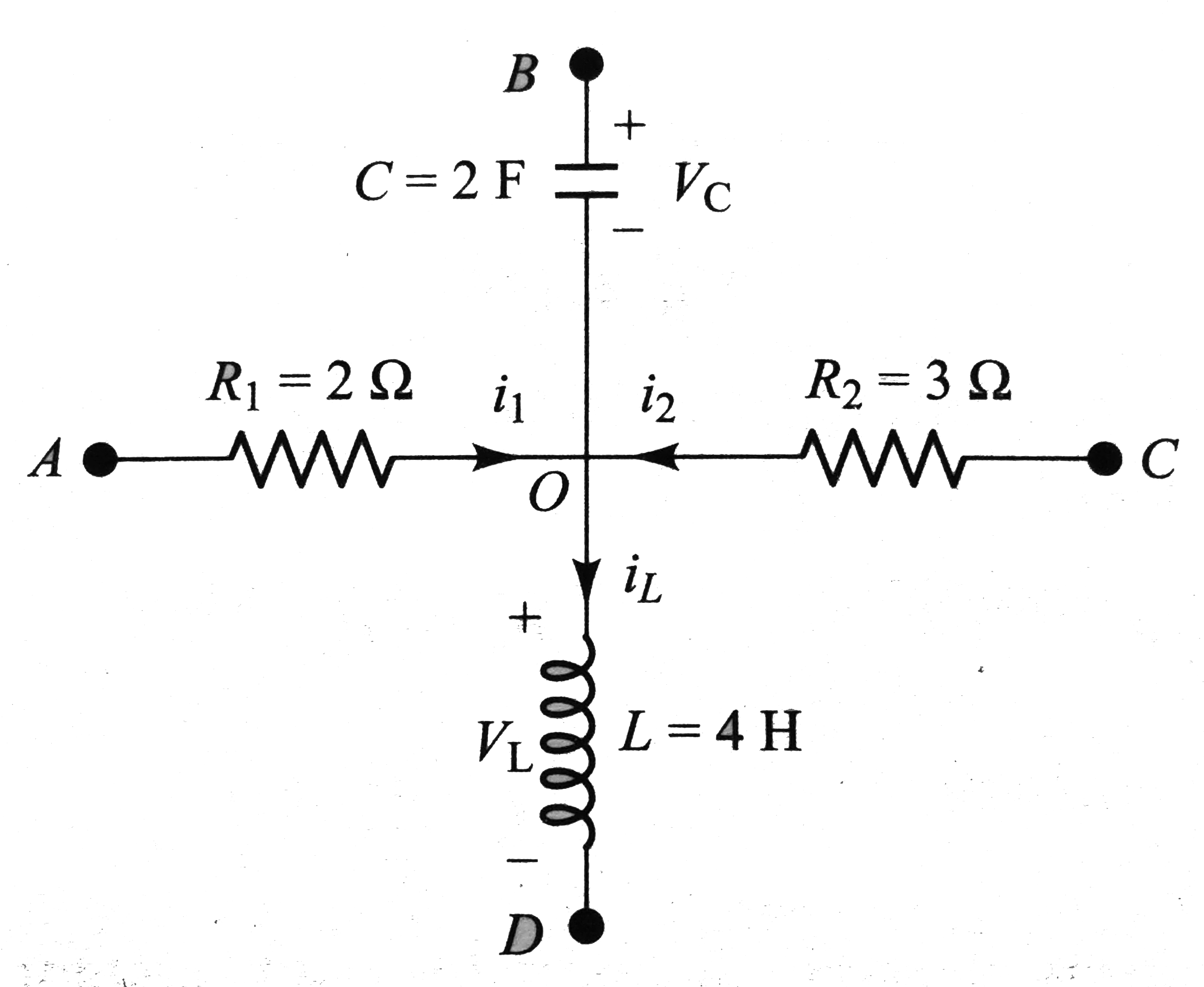
In the Figure shown i1=10e−2tA,i2=4A and VC=3e−2tV. Determine

a. iL and VL b. Vac,Vab,Vcd
8e−2tV
12e−3tV
17e−2tV
16e−2tV
The correct Answer is:C
Instanctaneous current in the capacitor,
q=CVC=(2)(3e−2t)=6e−2tA
Current, iC=dqdt=−12e−2tA
This current flows from B to O.
From KVL, we have
iL=i1+i2+iC=10e−2t+4−12e−2t
=(4−2t−2t)A=[2+2(1−e−2t)]A
iLvs. time graph is as shows in Fig lt
iL increases from 2A to 4A expontially.

VL=LdiLdt
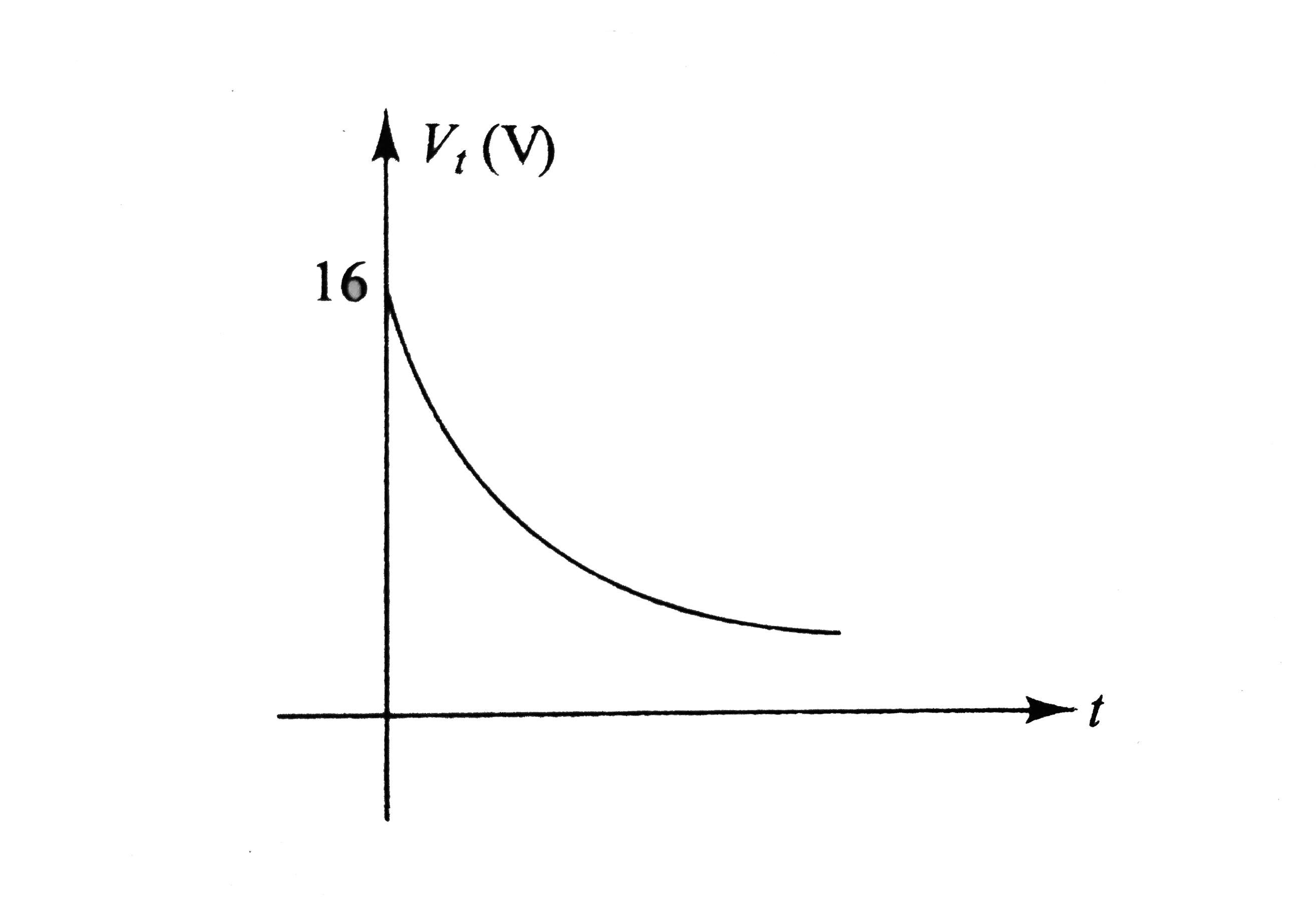
=(4)ddt(4−2e−2t)=16e−2tV
VL decreases exponentially from 16A to 0 as shows in Fig
To determine VAC, we begin from A and at C. From KVL,
we have

VA−i1R1+i2R2=VC
VA−VC=i1R1−i2R2
Substituting the values, we have
VAC=(10e−2t)(2)−(4)(3)
VAC=(20e−2t−12)V
At t=0, VAC=8V
At t=∞, VAC=−12V
Therefore, VAC decrease exponentially from 8V to 12V.
Similarly, we have from A to B
VA−i1R1+VC=VB
VAB=VA−VB=i1R1−VC 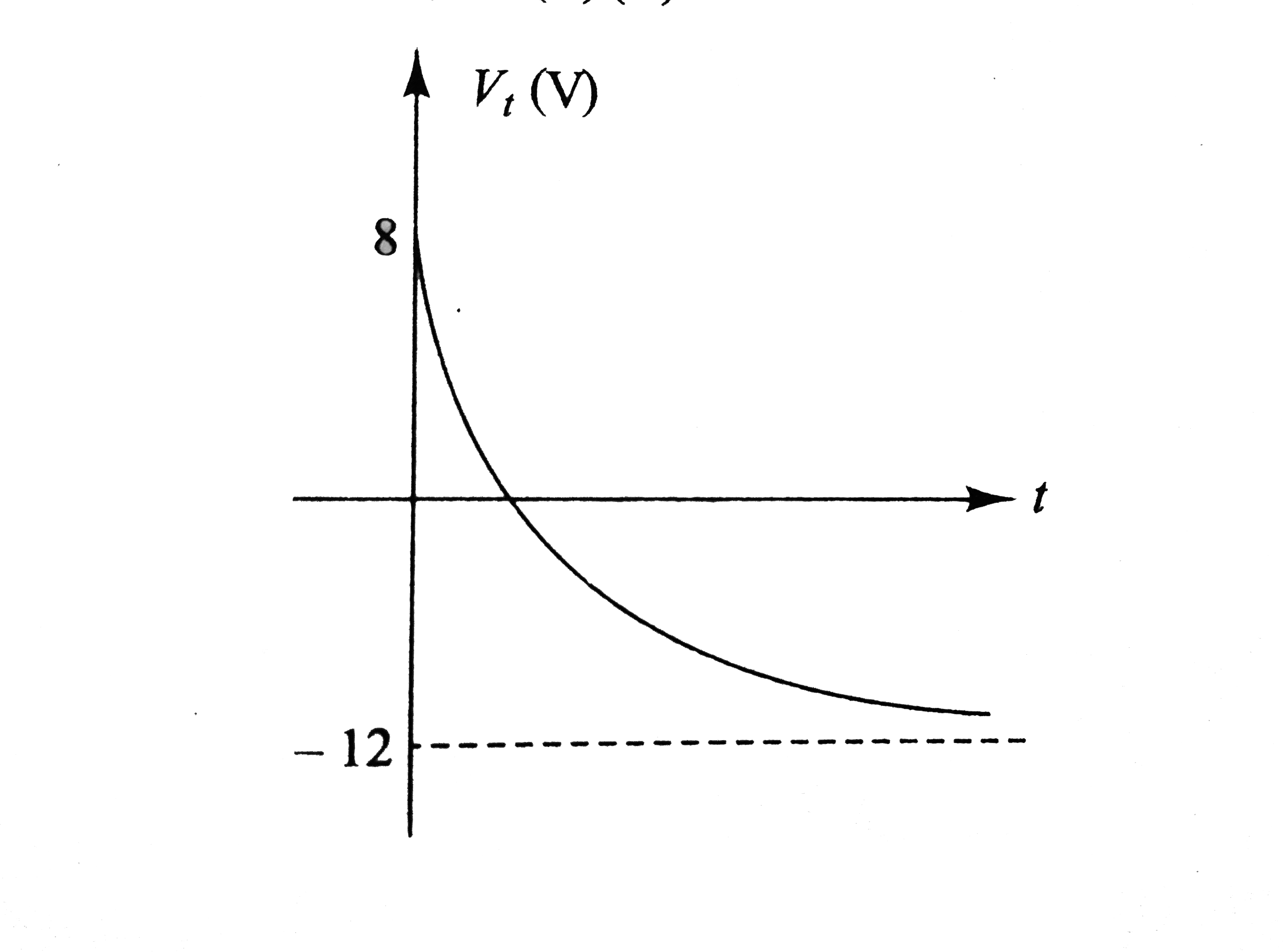
Substituting the values, we have
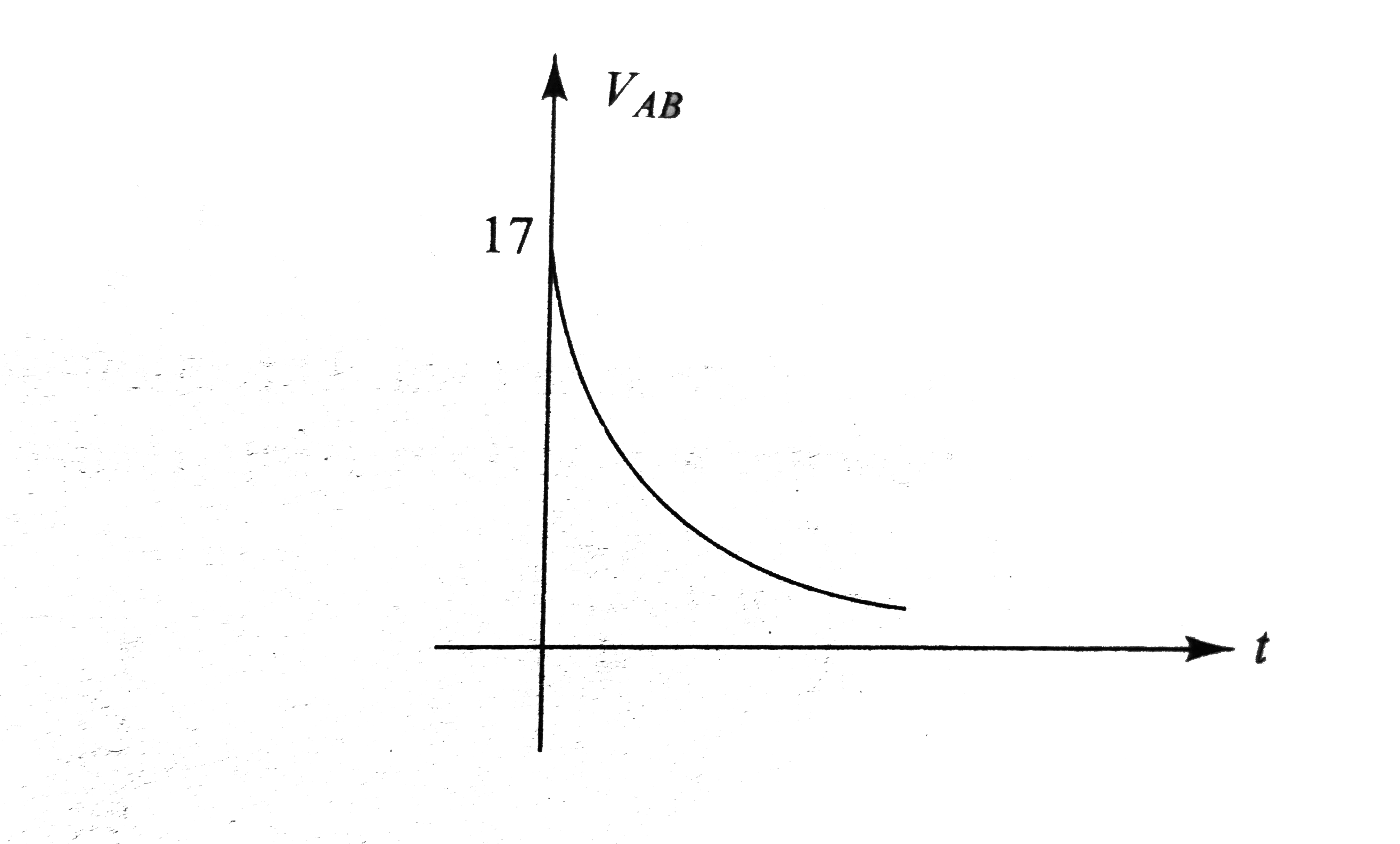
VAB=(10e−2t)(2)−3e−2t
VAB=17e−2tV
Thus, VAB decreases exponentially from 17V to 0.
As we move from C to D,
VC−i2R2−VL=VD
VCD=VC−VD=i2R2+VL
Substituting the values we have,
VCD=(4)(3)+16e−2t
VAD=(12+16e−2t)V
At t=0,VCD=28V
and at t=∞,VCD=12V
i.e., VCD decreases exponentially from 28V to 12V.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Knowledge Check
- Question 1 - Select One
In the figure shown i=10e−4tA. Find VL and Vab
 A−40eVB40eVC40eVD−40eV
A−40eVB40eVC40eVD−40eV
Similar Questions
In the figure shown i=10e−4tA. Find VL and Vab
 View Solution
View SolutionIn the figure shown i=10e−4tA. Find VL and Vab
 View Solution
View SolutionIn the figure shown Vab at t=1 is
 View Solution
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
the vartiation of potential difference across A and C(VAC) with time can be respresented asView SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
The variation of potential difference across C and D(VCD) with time can be expressed asView SolutionIn the circuit shown in figure
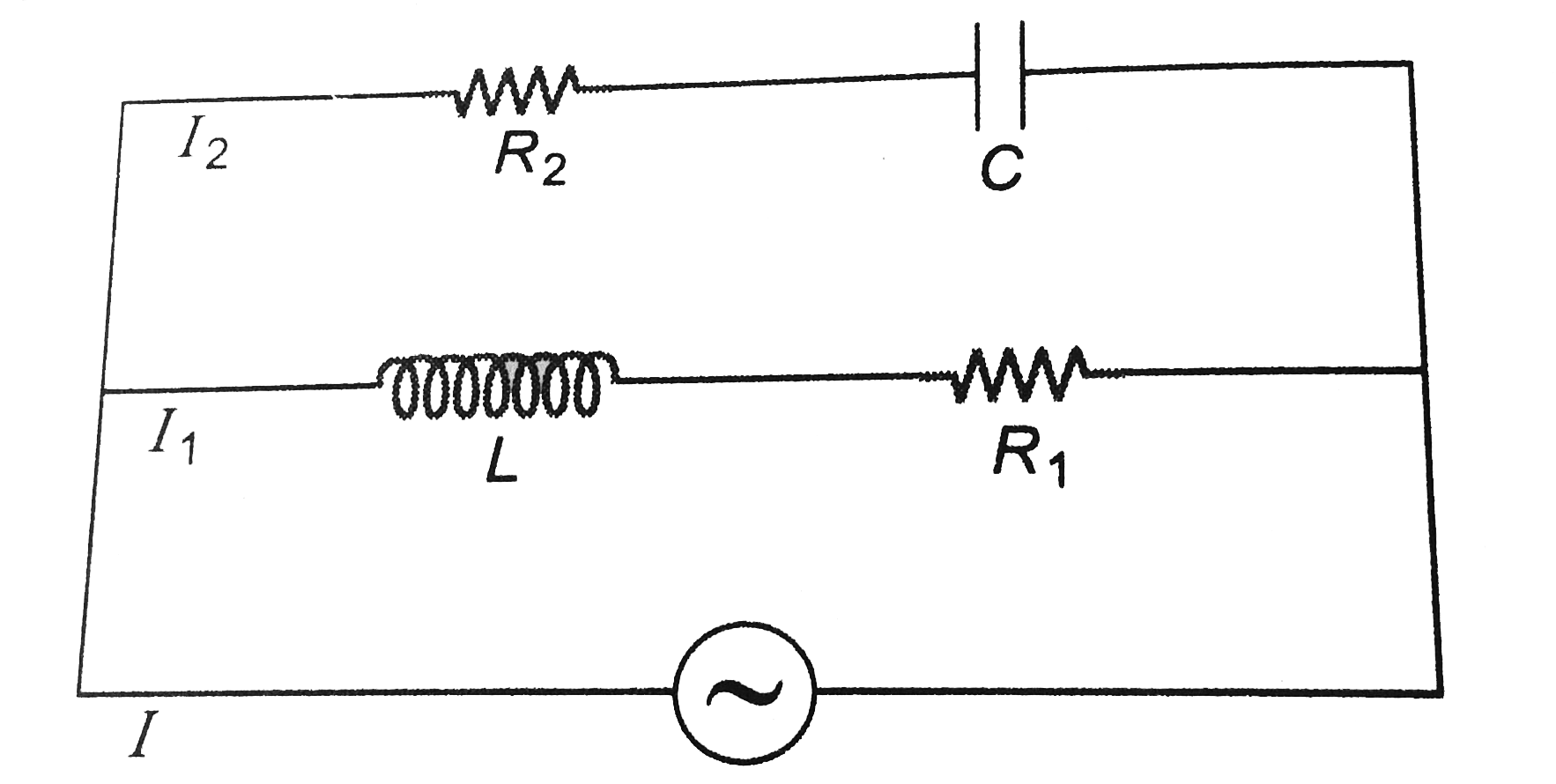
R1=30Ω,R2=40Ω,L=0.4H and C=13mF.
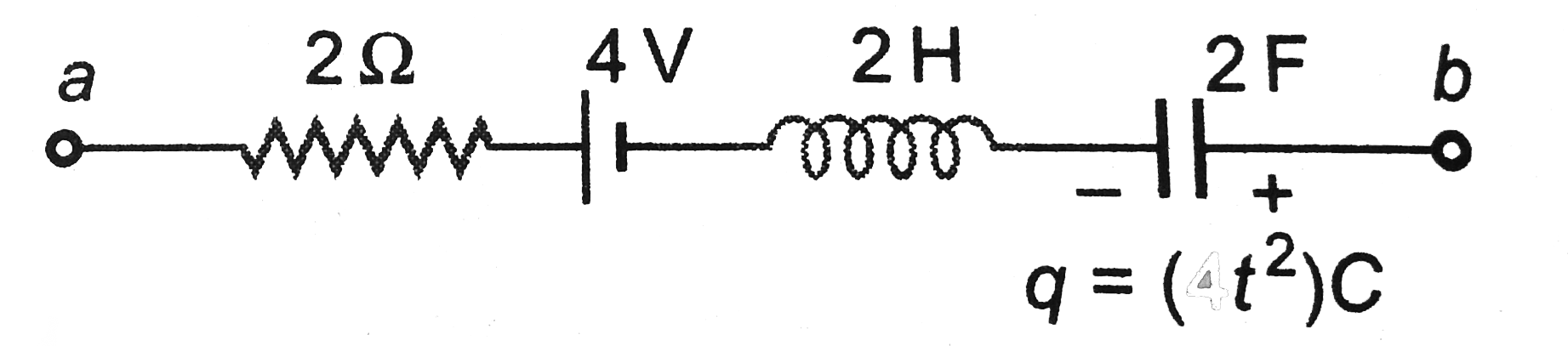
Find seven function of time I,I1,I2,VR1,VL,VR2 and VC. Also total power consumed in the circuit. In the given potential function V is in volts and omega rad/s V=200 sin(100t+30)View SolutionIn the circuit shown in figure q varies with time t as q=(16t2). Here q is in coulomb and t in second.
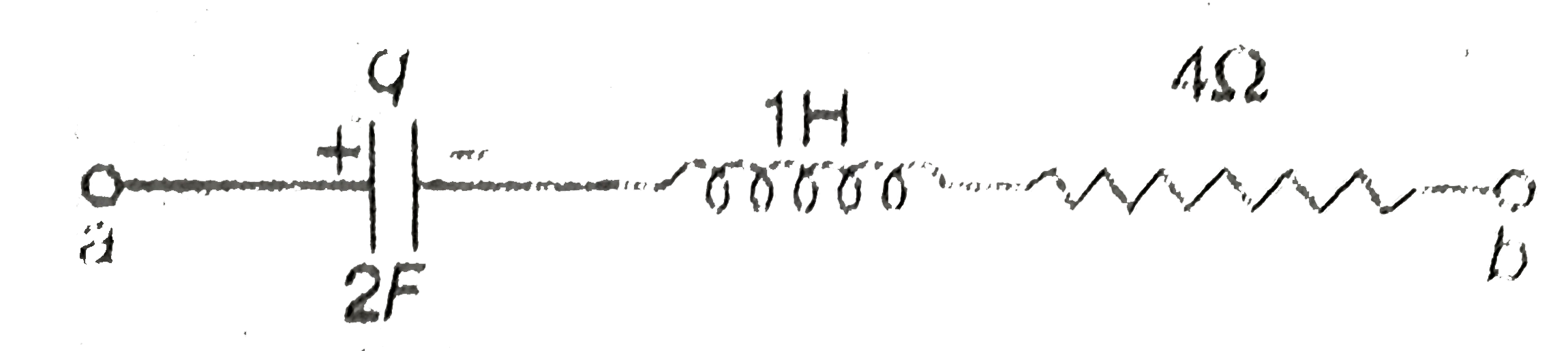
Find Vab=(Va−Vb)att=3sView SolutionGiven figure is the part of some circuit. Charge on the capacitor in the circuit is given by q=3(3−e−t), (coulomb) where t is time in seconds.
Let VA, VB and VC be the potentials of points A, B and C, respectively. At t=0 if VA=5V and a constant current i0=1Amp flows through R=1Ω, then find the VP (in volt)
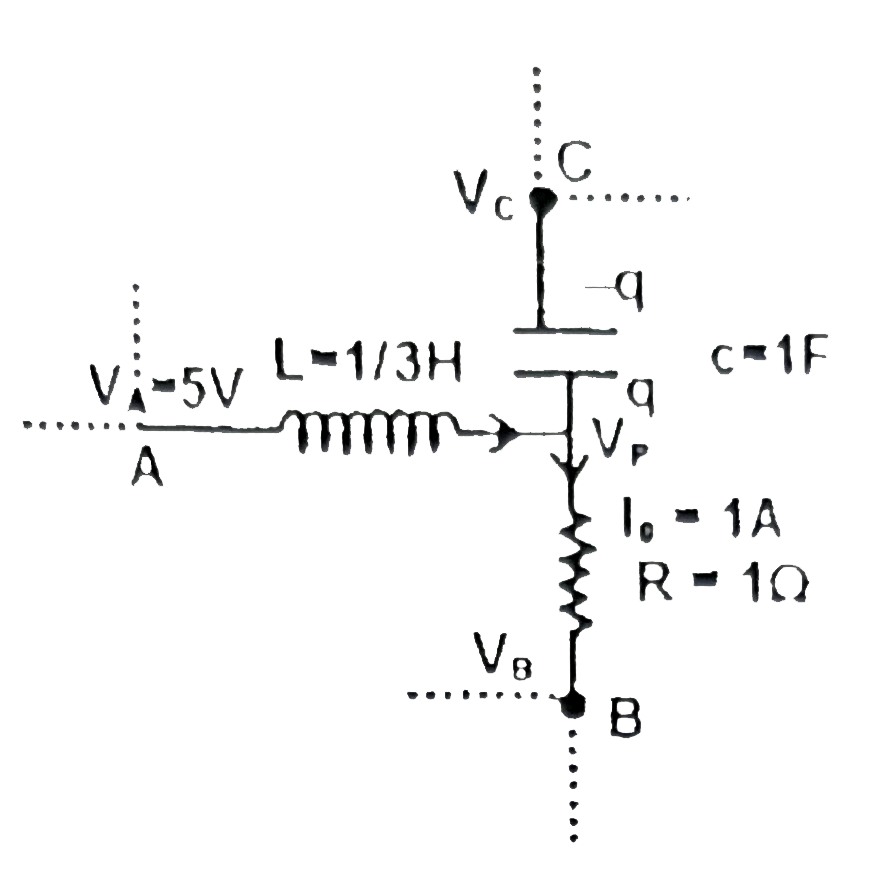 View Solution
View SolutionIn the figure shown, the reading of voltmeters are V1=40V,V2=40V and V3=10V. Find
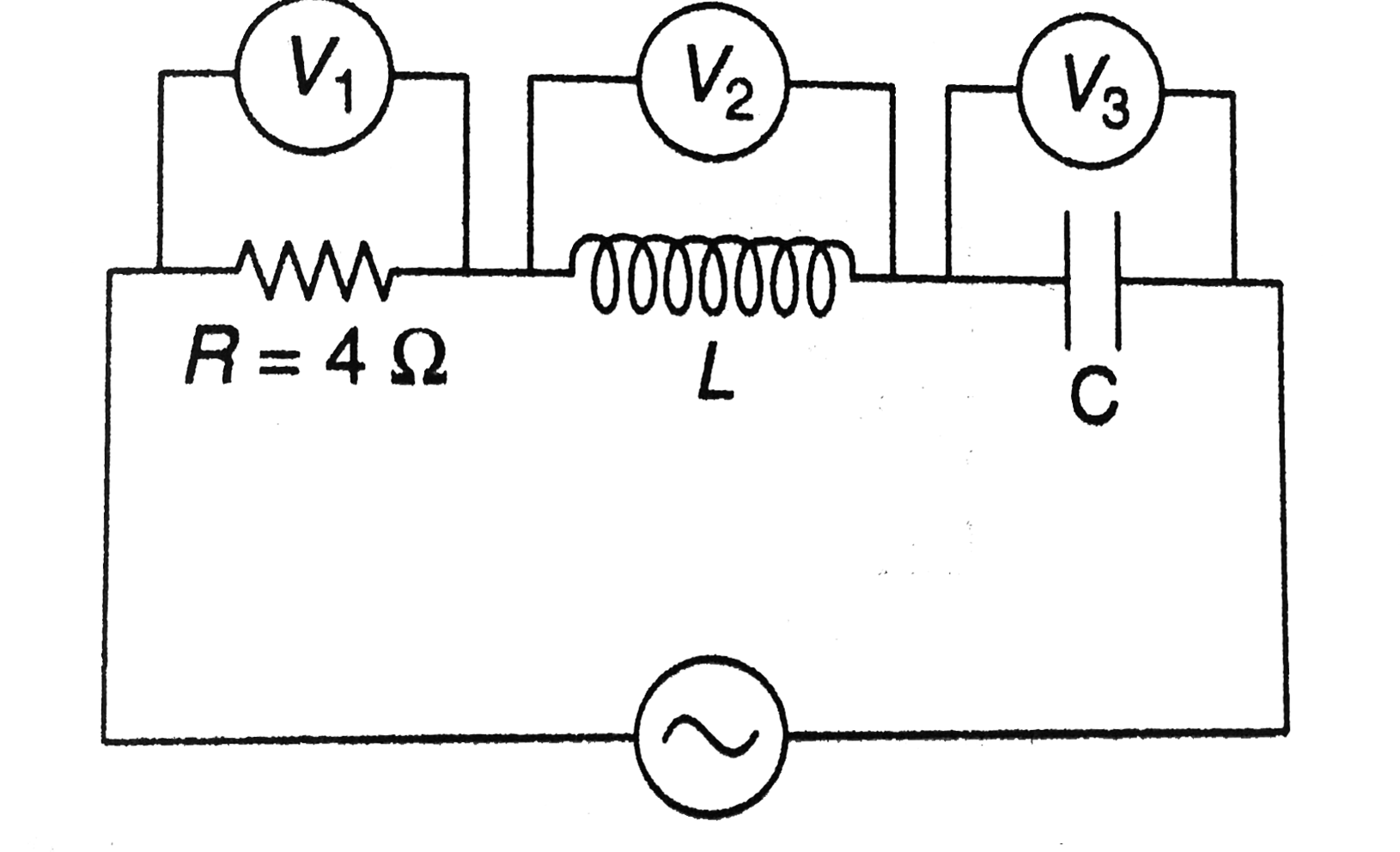
(a) the peak value of current
(b) the peak value of emf
(c) the value of L and C.View Solution

