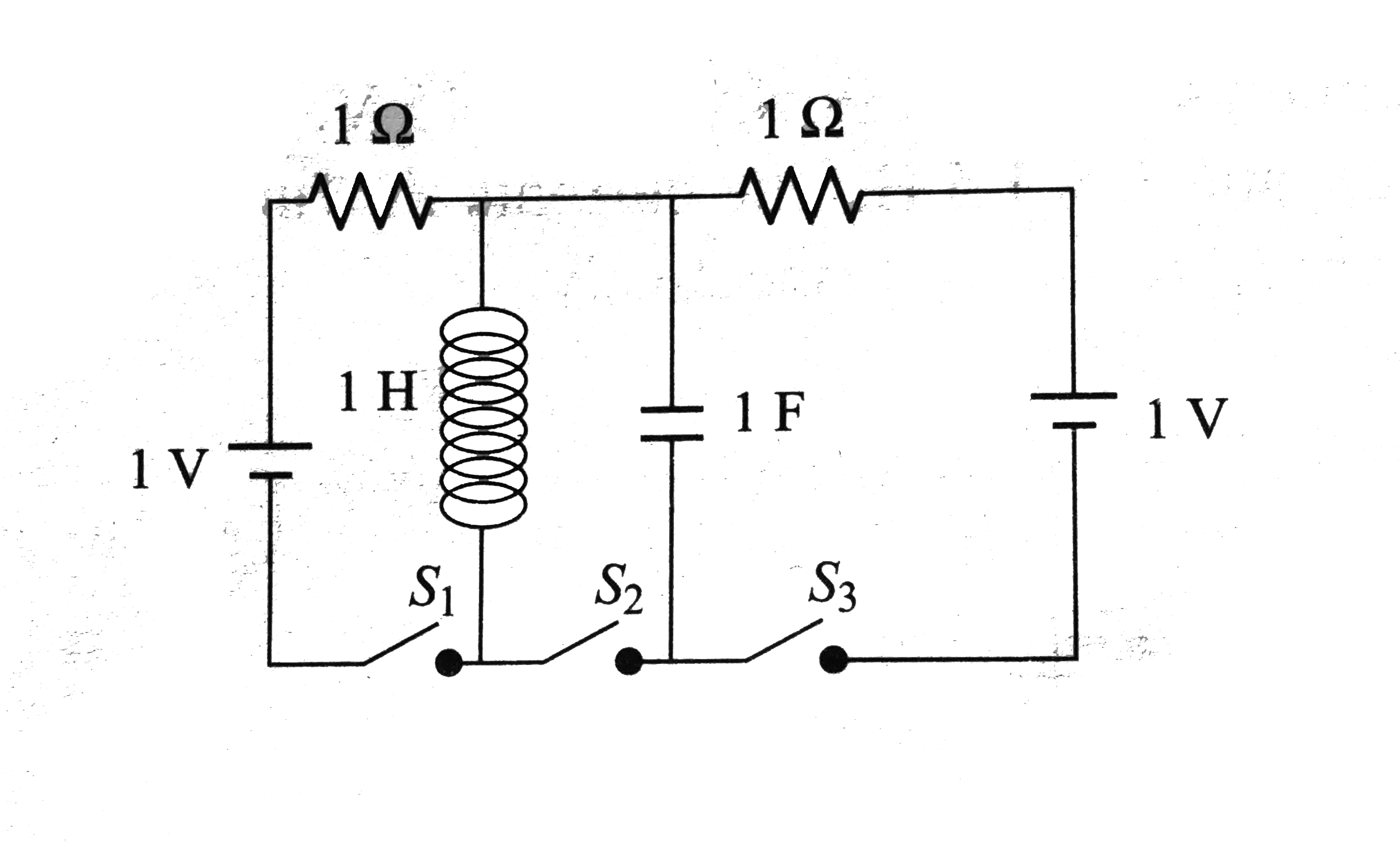
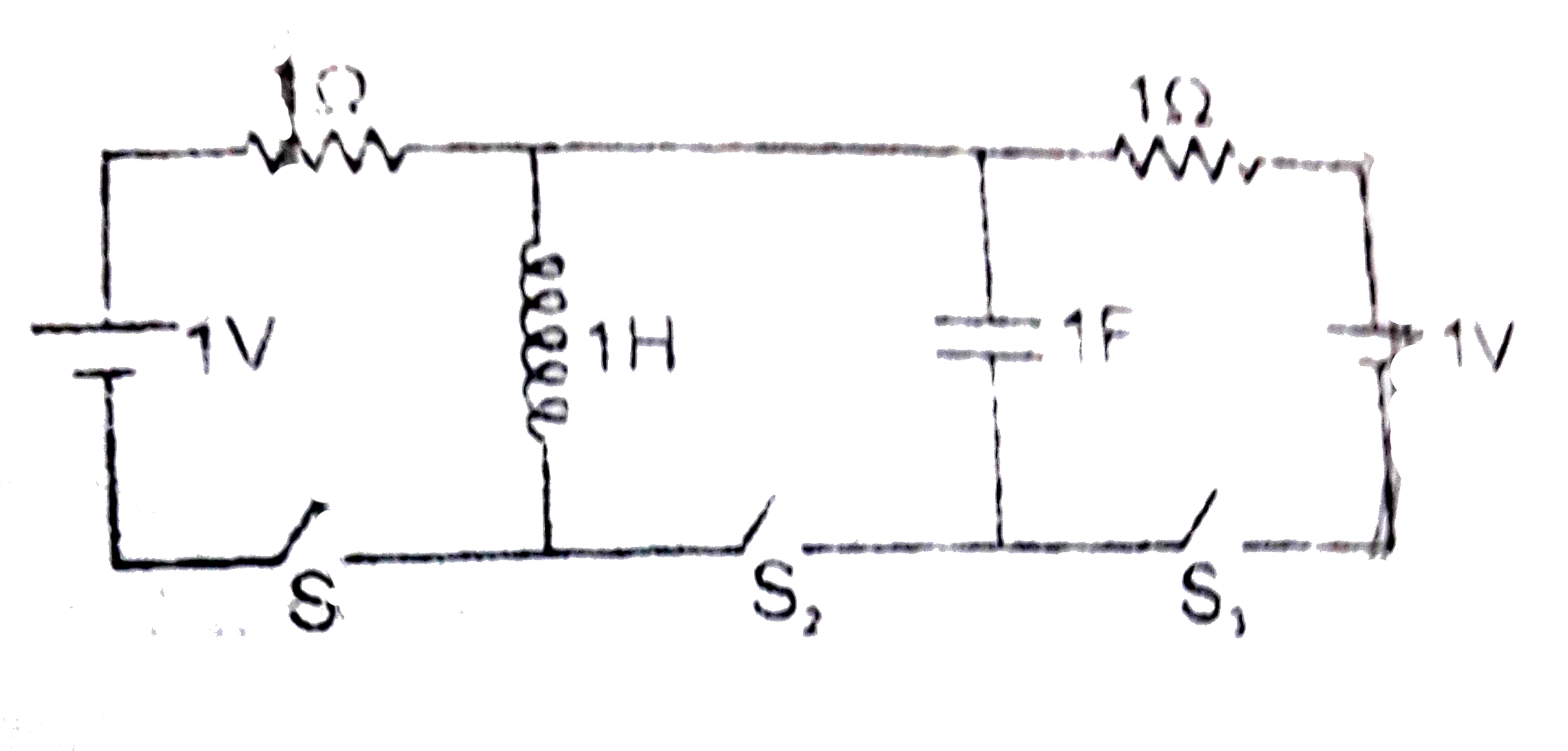
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the charge on the upper plate of the capacitor as a funtion of time
√2(1−1e)sin(t+3π4)
√2(1−1e)sin(t+π4)
√3(1−1e)sin(t+π4)
√3(1+1e)sin(t+π4)
The correct Answer is:A
S1 and S2 are closed for 1s.
Charge on capacitor,
q=CE(1−e−t/RC)=1−1e (i)
The current in inductor,
I=ER(1−e−t/RC)=1−1e(ii)
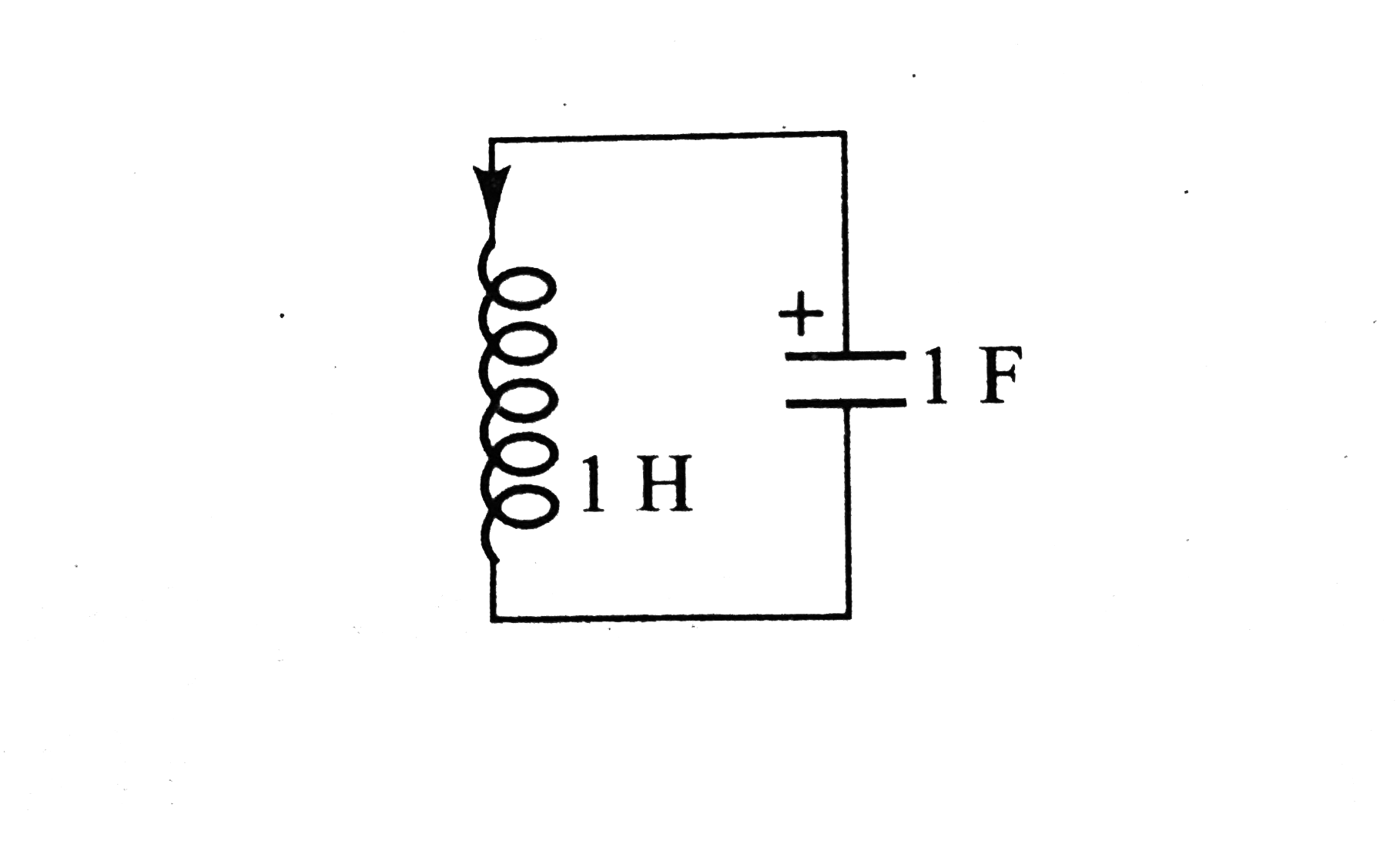
Now S1 and S3 are opened and S2 is closed,
It is LC circuit,
q=qmaxsin(ωt+ϕ) (iii)
I=(qmax)ωcos(ωt+ϕ) (iv)
As total energy (Magnetic + electrical) is constant
12LI2max=12q2maxC=12LI2+12q2C (v)
qmax=√2(1−1e) (vi)
Imax=√2(1−1e) (vii)
From (iii) at t=0, we get
(1−1e)=√2(1−1e)sinϕ⇒=π4 or 3π4
After closing S2, circuit will be as shows. Direction of current shows that charge on capacitor will be decreaseing. Hence ϕ=3π/4
q=√2(1−1e)sin(ωt+3π4)
where, ω=1√LC=1
q=√2(1−1e)sin(t+3π4)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the maximum charge on the capacitor
View SolutionIn the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
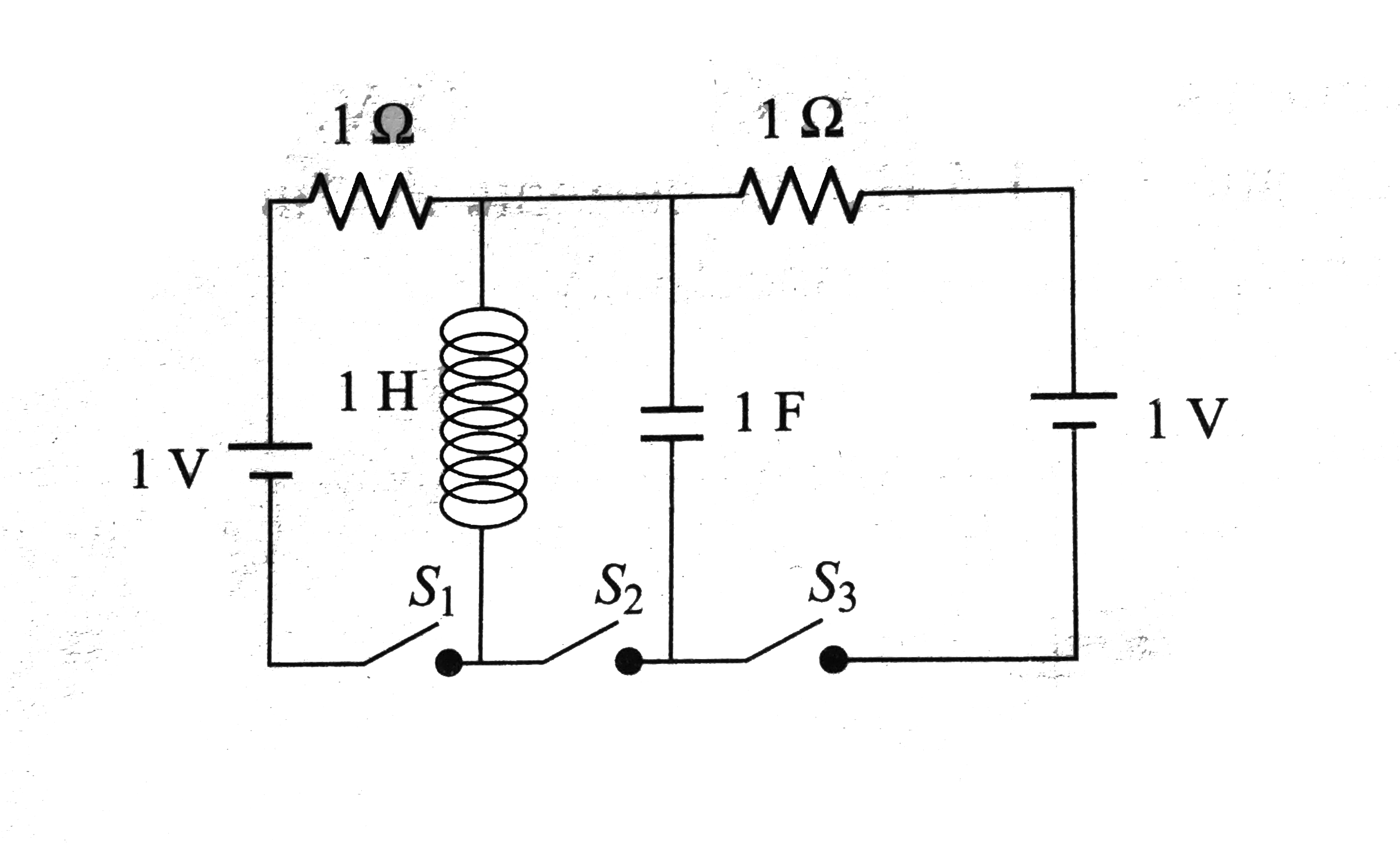
the maximum current in the circuit containing inductor and capacitor (only S2 is closed)
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
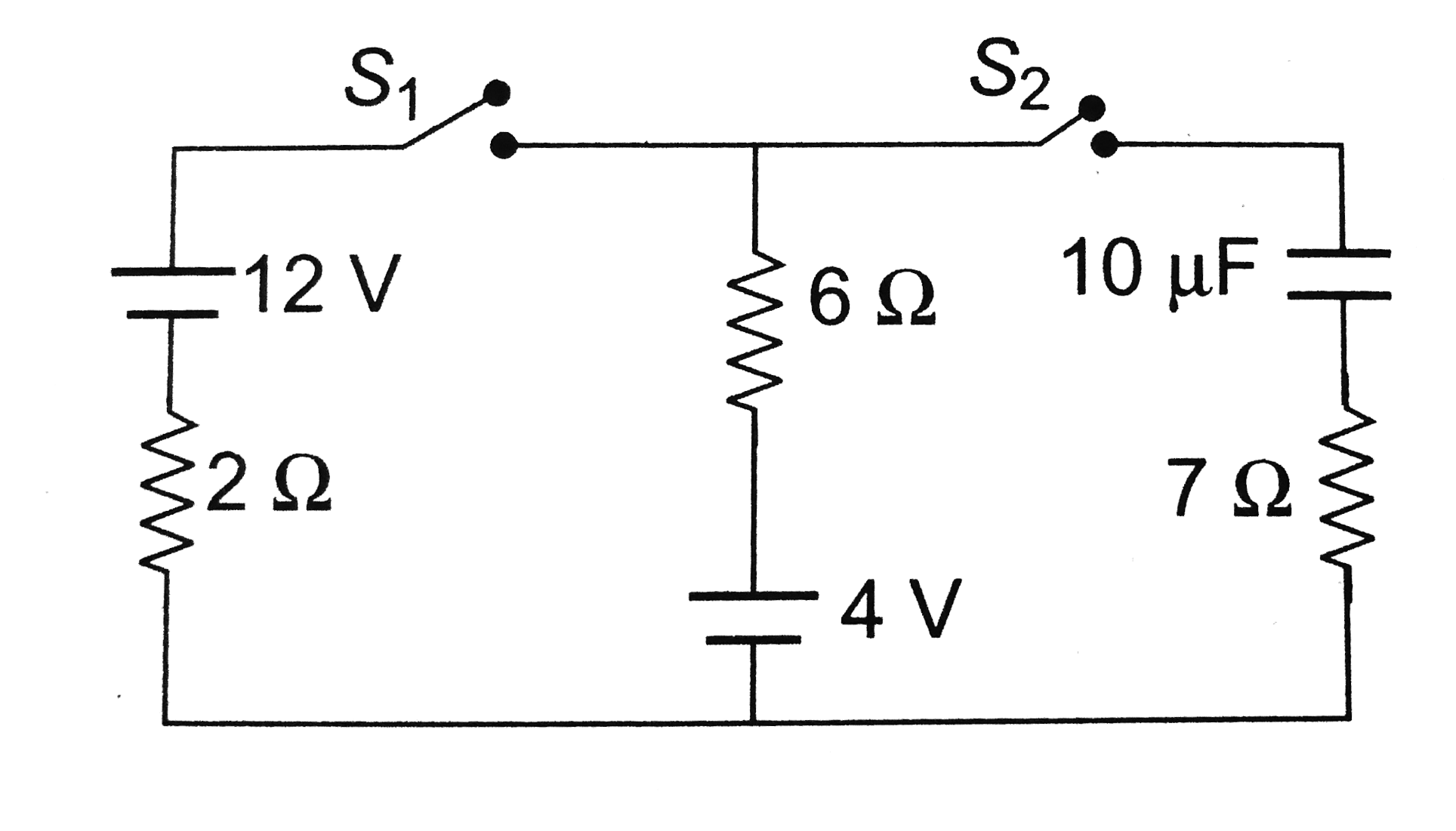
View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View SolutionIn the circuit shown, S2 is closed first and is kept closed for a long time. Now S1 is closed. Just after that instant the current through S1is

View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

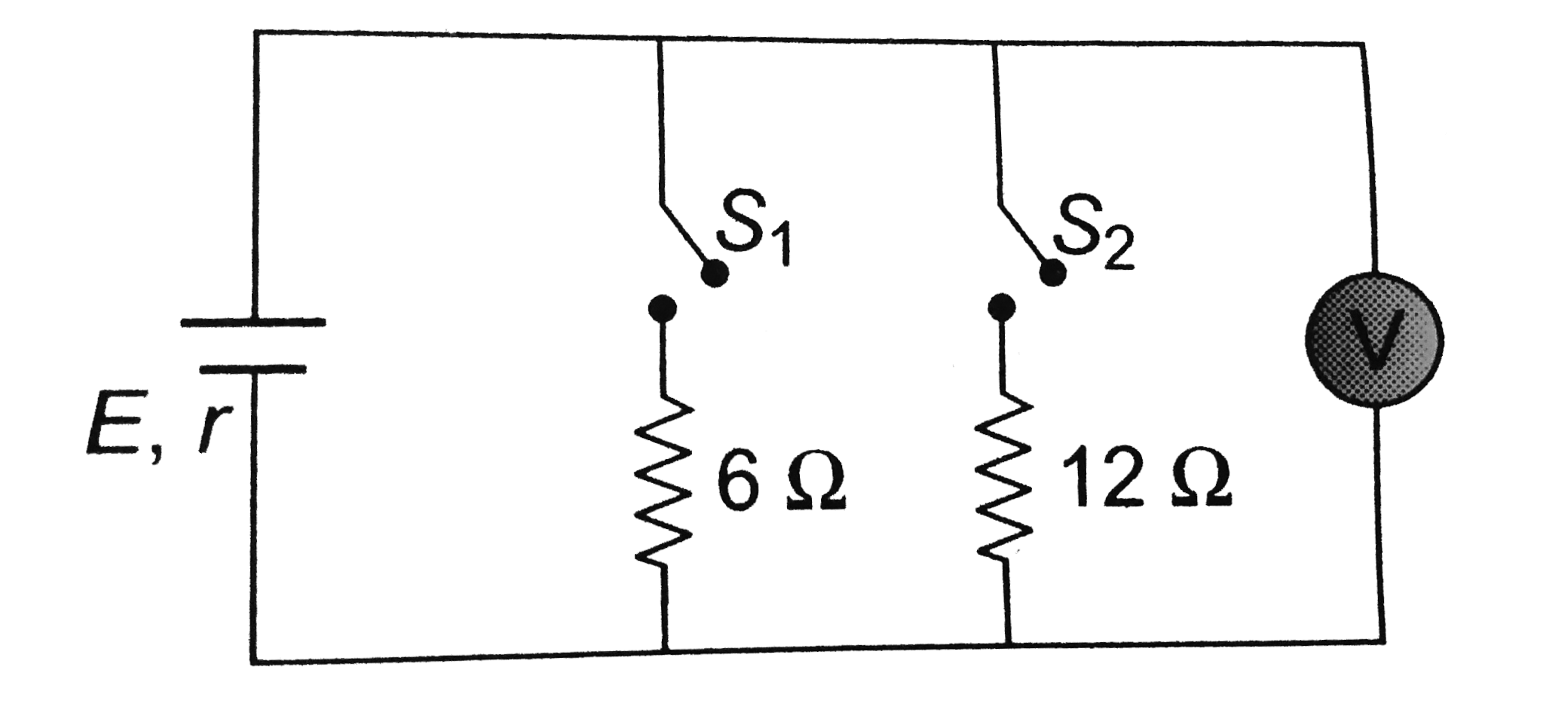
View SolutionIn the circuit shown, when switch S1 is closed and S2 is open, the ideal voltmeter shows a reaiding of 18V. When switch S2 is closed and S1 is open, the reading of voltmeter is 24V. When S1 and S2 both are closed, the voltmeter reading will be
View SolutionIn the circult shown
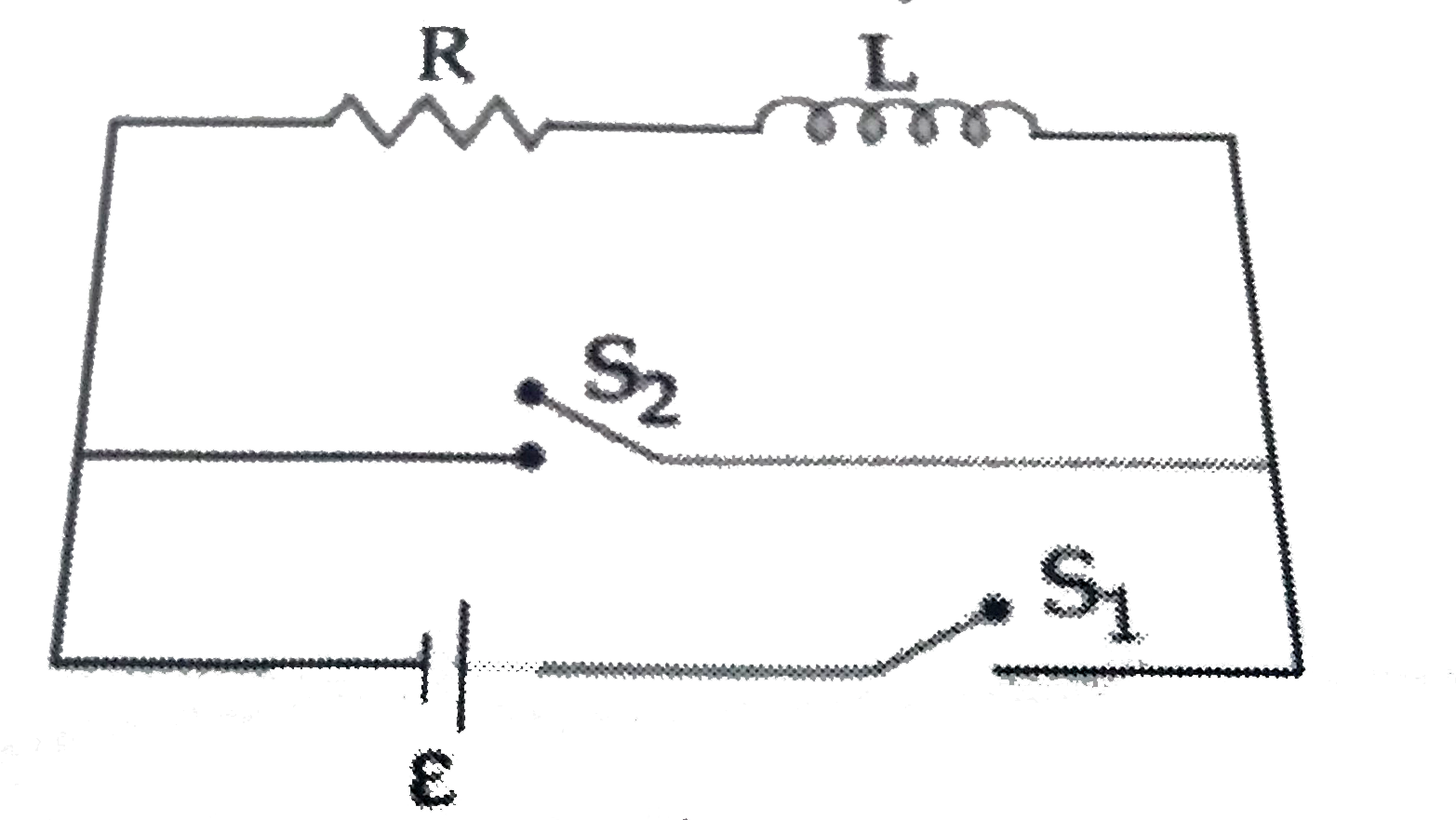 the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
View Solution
