In exercise, let us take the position of mass when the spring is unstreched as x=0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t=0), the mass is
a} at the mean position
b} at the maximum stretched position and
c} at the maximum compressed position In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase ?
Here, a=20cm,ω=√km=√12003=20s−1
a) As time is noted from the mean position, hence using x=asinωt, we have x=2sin20t.
b) At maximum stretched position, the body is the extreme right position, with an initial phase of π2 rad. Then
x=asin(ωt+π2)
=acosωt=2cos20t
c) At maximum compressed position, the body is at the extreme left position, with an initial phase of 3π2 rad.
Then x=asin(ωt+3π2)
=−acosωt
=−2cos20t
Similar Questions
In exercise 14.9 let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position.
(b) at the maximum stretched position, and
( c ) at the maximum compressed position.
IN what way do these functions for SHM differ from each other, in frequency in amplitude or the initial phase ?View SolutionIn example 34, let us take the position of the mass, when the spring is unstretched, as x=0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass, if at the moment we start the stop watch (t=0), the mass is (i) at the mean position (ii) at the maximum stretched position (iii) at the maximum compressed position.
In what do these different functions of SHM differ ? Frequency, amplitude or initial phase ?View Solution
Knowledge Check
- Question 1 - Select One
The inclination of the line x−y+3=0 with the positive direction of x-axis is
A45∘B135∘C−45∘D−135∘ - Question 2 - Select One
The inclination of the line x−y+3=0 with the positive direction of x-axis is :
A45∘B135∘C−45∘D−135∘ - Question 3 - Select One
This is the position graph of a mass on a spring what can you say about the velocity and the force at the instant indicated by the dashed line ? Positive direction is to right
 AVelocity is zero , force is to the rightBVelocity is positive , force is to the rightCVelocity is negative , force is to the rightDVelocity is zero , force is to the left
AVelocity is zero , force is to the rightBVelocity is positive , force is to the rightCVelocity is negative , force is to the rightDVelocity is zero , force is to the left
An impulsive force gives an initial velocity of- 1.0ms−1 to the mass in the unstretched spring position [sec Fig. 16.2]. What is the amplitude of motion ? Give x as a function of time t for the oscillating mass. Given m=3 kg and k=1200Nm−1.
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x-axis. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)
 View Solution
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
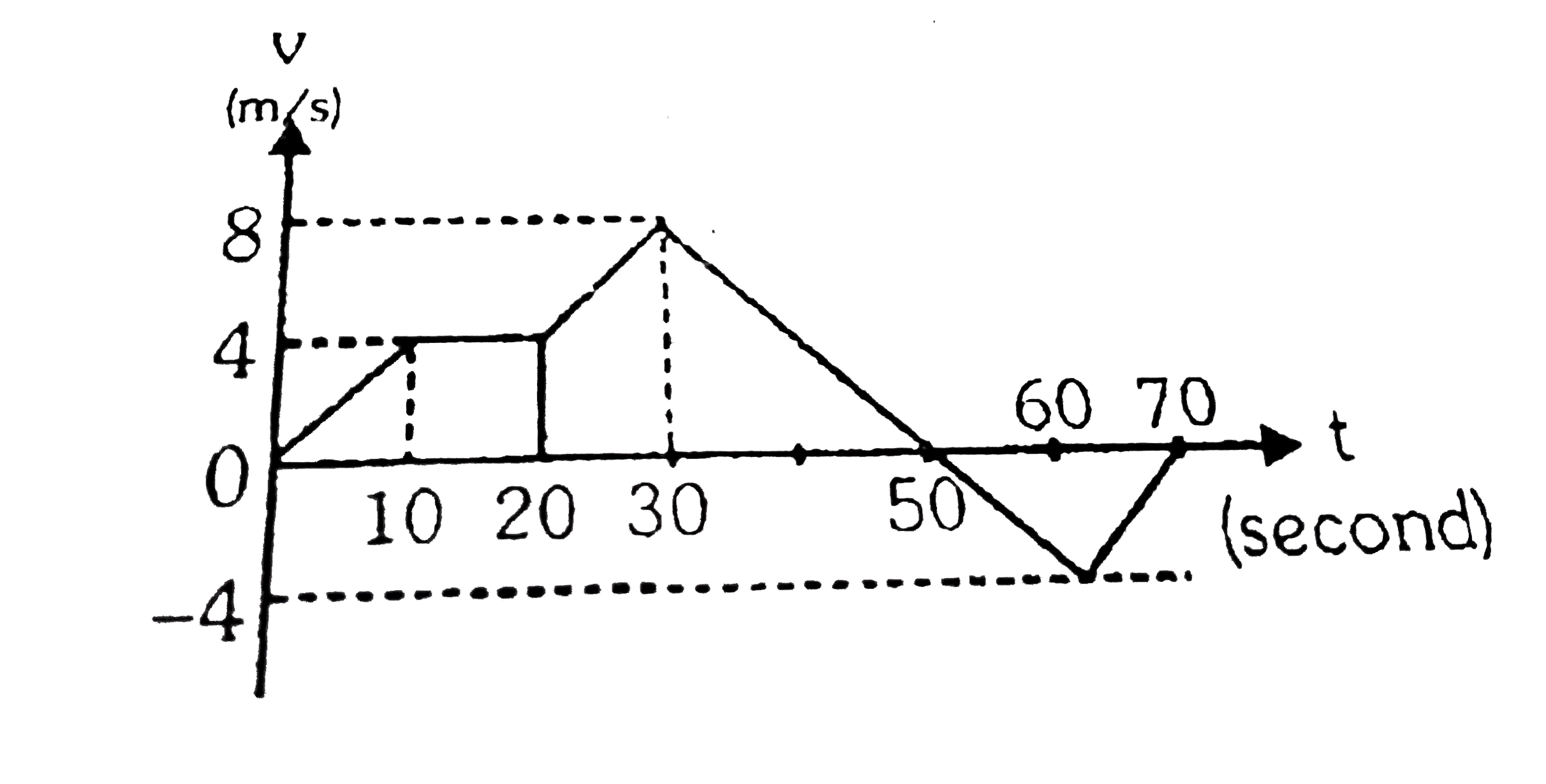
The maximum displacement from the starting position will be :-View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.

The maximum displacement from the starting position will be :-View SolutionA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)
 View Solution
View Solution
