Derive an expression for the acceleration due to gravity at a depth d below the Earth's surface.
Let a body P of mass m be situated at a depth h below the earth's surface.
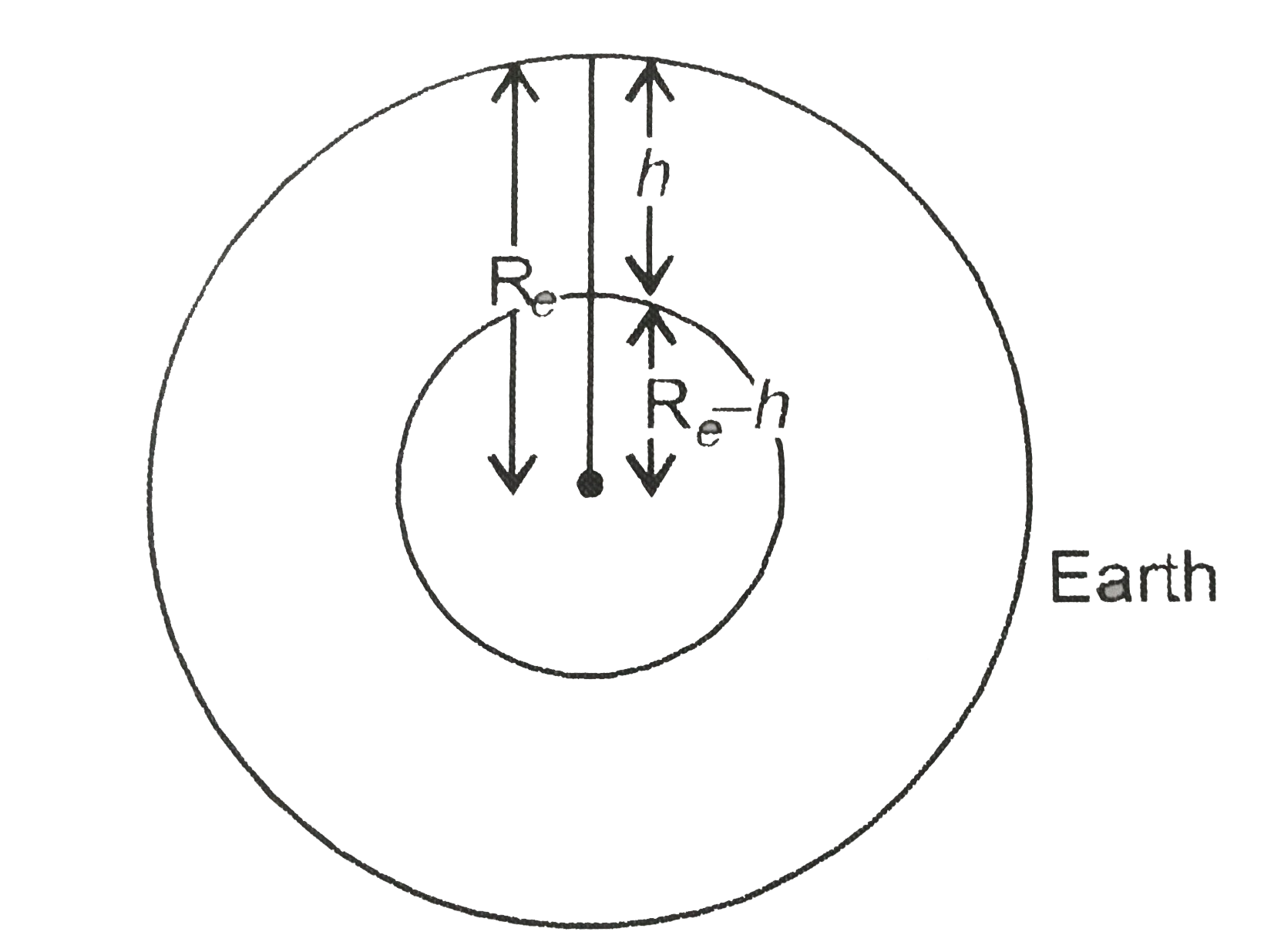
The gravitational force of attraction on a body inside a spherical shell is always zero. Therefore, the body P experiences gravitational attraction only due to the inner solid sphere. The mass of this sphere is
M'=volume×density=43π(Re−h)3ρ ...(i)
where ρ is mean density of the earth. Therefore, according to Newton's law of gravitation, the force of attraction on the body P is
GM'm(Re−h)2=G43π(Re−h)3ρm(Re−h)2 [Using equation (i)]
=43πG(Re−h)ρm
This force must be equal to the weight of the body mg', where g' is the acceleration due to gravity at a depth h below the surface of the earth. Thus,
mg'=43πG(Re−h)ρm ...(ii)
Similarly, if a body be at the surface of the earth (h = 0) where acceleration due to gravity is g, then
mg=43πGReρm ...(iii)
Dividing equation (ii) by (iii), we have
g'g=Re−hRe
⇒ g'=g(1−hRe)
This is the expression for acceleration due to gravity at depth h below the earth surface.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Acceleration due to gravity at a depth equal to half the radius of earth from its surface is
Ag2B3g2Cg4D3g4 - Question 2 - Select One
The acceleration due to gravity on the surface of earth varies
Adirectly with longitudeBdirectly with latitudeCinversely with longitudeDinversely with latitude
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionDraw graphs showing the variation of acceleration due to gravity with depth below the earth's surface.
View SolutionDraw graphs showing the variation of acceleration due to gravity with depth below the earth's surface.
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View SolutionLet g be the acceleration due to gravity on the earth's surface.
 View Solution
View SolutionDraw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View Solution
