Derive an expression for the acceleration due to gravity at a depth d below the Earth's surface.

Video Solution

Text Solution

Verified by Experts

Let a body P of mass m be situated at a depth h below the earth's surface.

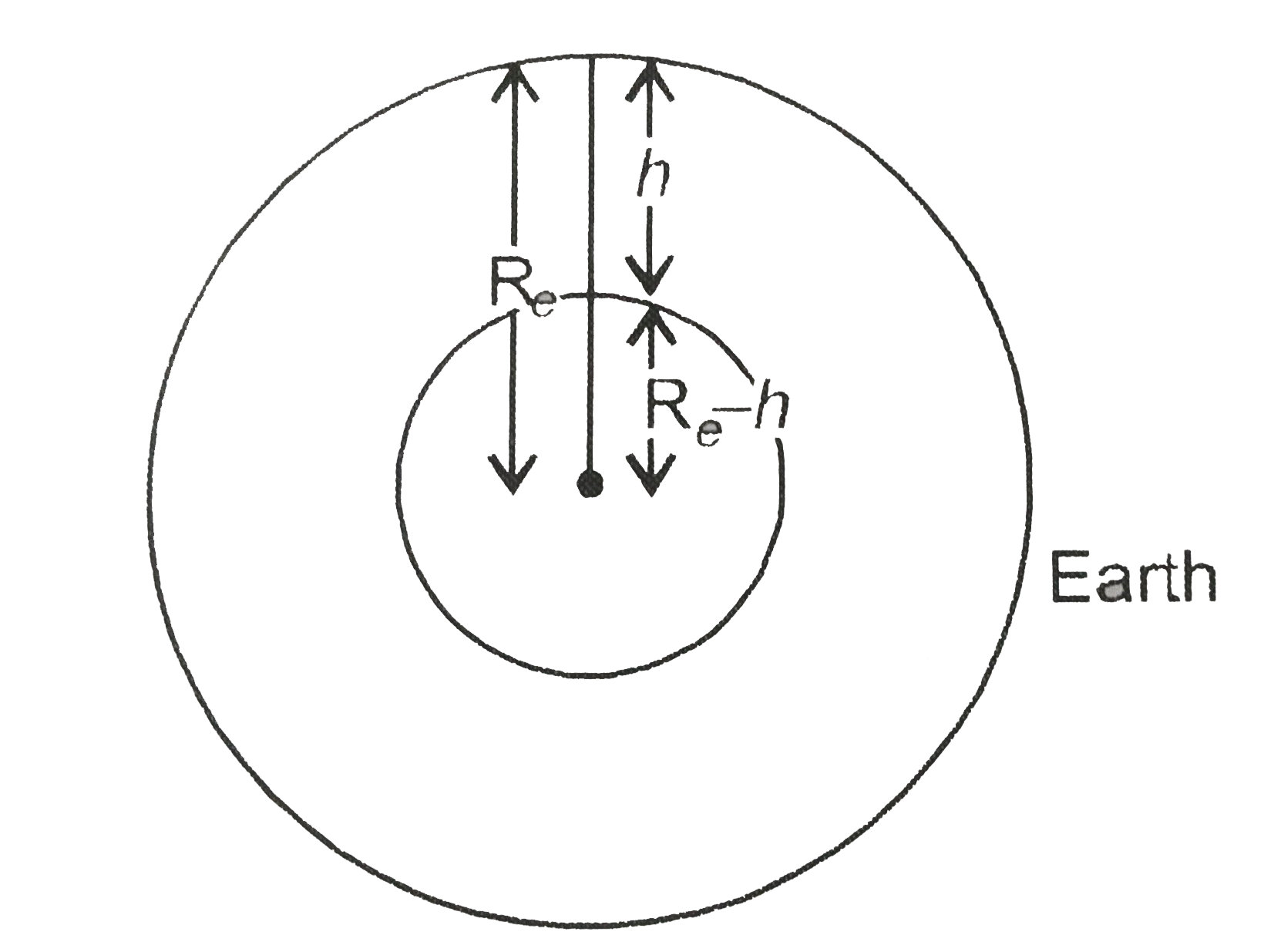
The gravitational force of attraction on a body inside a spherical shell is always zero. Therefore, the body P experiences gravitational attraction only due to the inner solid sphere. The mass of this sphere is
$M' = volume \times density = \frac{4}{3} π {(R_{e} - h)}_{e}^{3} ρ ... (i)$
where $ρ$ is mean density of the earth. Therefore, according to Newton's law of gravitation, the force of attraction on the body P is
$\frac{GM' m}{{(R_{e} - h)}_{e}^{2}} = G \frac{\frac{4}{3} π {(R_{e} - h)}_{e}^{3} ρ m}{{(R_{e} - h)}_{e}^{2}} [Using equation (i)]$
$= \frac{4}{3} π G (R_{e} - h) ρ m$
This force must be equal to the weight of the body mg', where g' is the acceleration due to gravity at a depth h below the surface of the earth. Thus,
$m g' = \frac{4}{3} π G (R_{e} - h) ρ m ... (i i)$
Similarly, if a body be at the surface of the earth (h = 0) where acceleration due to gravity is g, then
$m g = \frac{4}{3} π G R_{e} ρ m ... (i i i)$
Dividing equation (ii) by (iii), we have
$\frac{g'}{g} = \frac{R_{e} - h}{R_{e}}$
$\Rightarrow g' = g (1 - \frac{h}{R_{e}})$
This is the expression for acceleration due to gravity at depth h below the earth surface.

Updated on:21/07/2023

Acceleration due to gravity at a depth equal to half the radius of earth from its surface is
A $\frac{g}{2}$
B $\frac{3 g}{2}$
C $\frac{g}{4}$
D $\frac{3 g}{4}$
The acceleration due to gravity on the surface of earth varies
Adirectly with longitude
Bdirectly with latitude
Cinversely with longitude
Dinversely with latitude