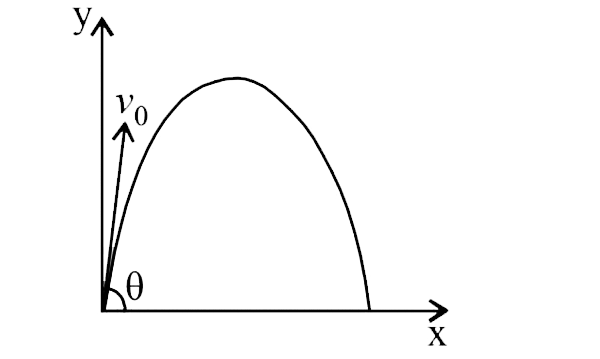
A small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.

As time of fight T=2υ0sinθg,
therefore, at t<υ0sinθg, particle has not reached the maximum height. Let →r be position vector the particle as shown in Fig.

→r=→ut−12→gt2
=(υ0cosθˆi+υ0sinθˆj)t−12>2ˆj
→r=υ0cosθ(t)ˆi+(υ0sinθ(t)−12>2)ˆj
and →υ=→u−→gt
=υcosθˆi+υθˆj−>ˆj
=υ0cosθˆi+(υ0sinθ−>)ˆj
Angular momentum of particle,
→L=m(→r×→υ) ..(i)
Now,
→r×→υ∣∣
∣
∣∣ˆiˆjˆkυ0cosθ(t)υ0sinθ(t)−12gt20υ0cosθ(υ0sinθ−gt)0∣∣
∣
∣∣
=ˆi(0−0)−ˆj(0−0)
+ˆk[υ20cosθsinθ(t)−υ0cosθgt2
−υ20cosθsinθt+12υ0cosθgt2]
→r×→υ=−12υ0cosθgt2ˆk
From (i),
→L=−12mgυ0t2cosθˆk
Related Playlists
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE B2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE C2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE A2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A small particle of mass m is projected at an angle θ with the x- axis with an initial velocity v0 in the x−yplane as shown in the figure . At a time t<v0sinθg, the angular momentum of the particle is
where ˆi,ˆjandˆk are unit vectors along x,yandz - axis respectively.
 View Solution
View SolutionA small particle of mass m is projected at an angle θ with the x-axis, with initial velocity v0 in the x-y plane. Just before time 2v0sinθg , the angular momentum of the particle about the point of projection is
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionA particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View SolutionIf a particle of mass m is moving with constant velocity v parallel to x-axis in x−y plane as shown in fig. Its angular moment with respect to origin at any time t will be
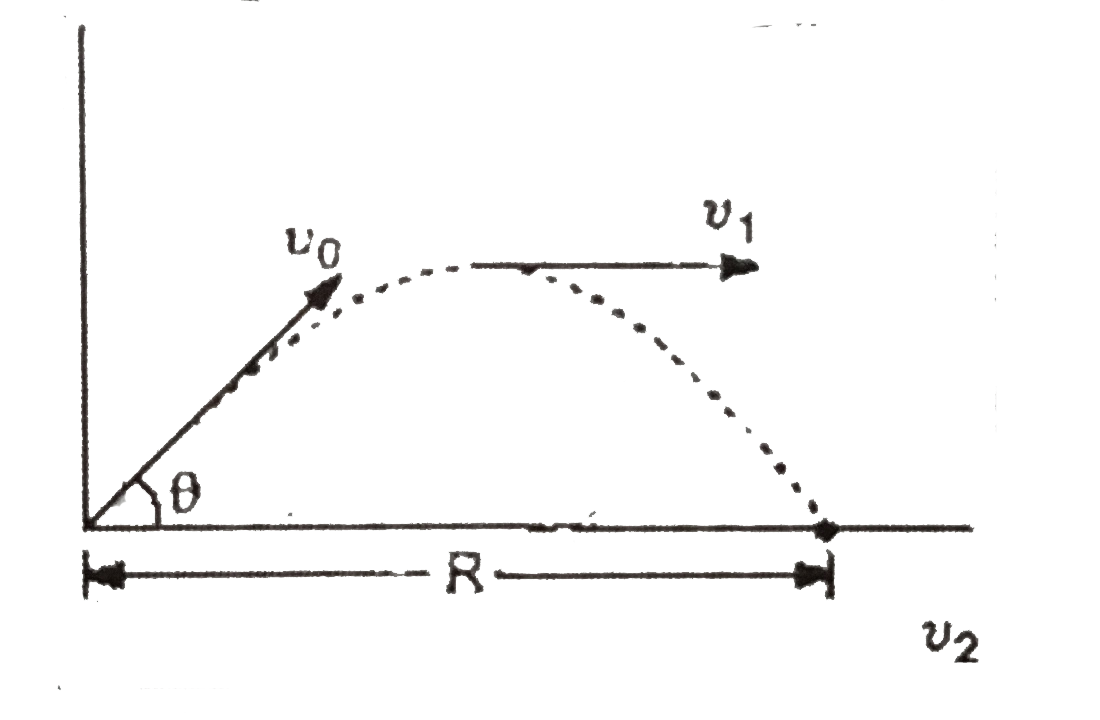
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
 View Solution
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strkes the ground again.
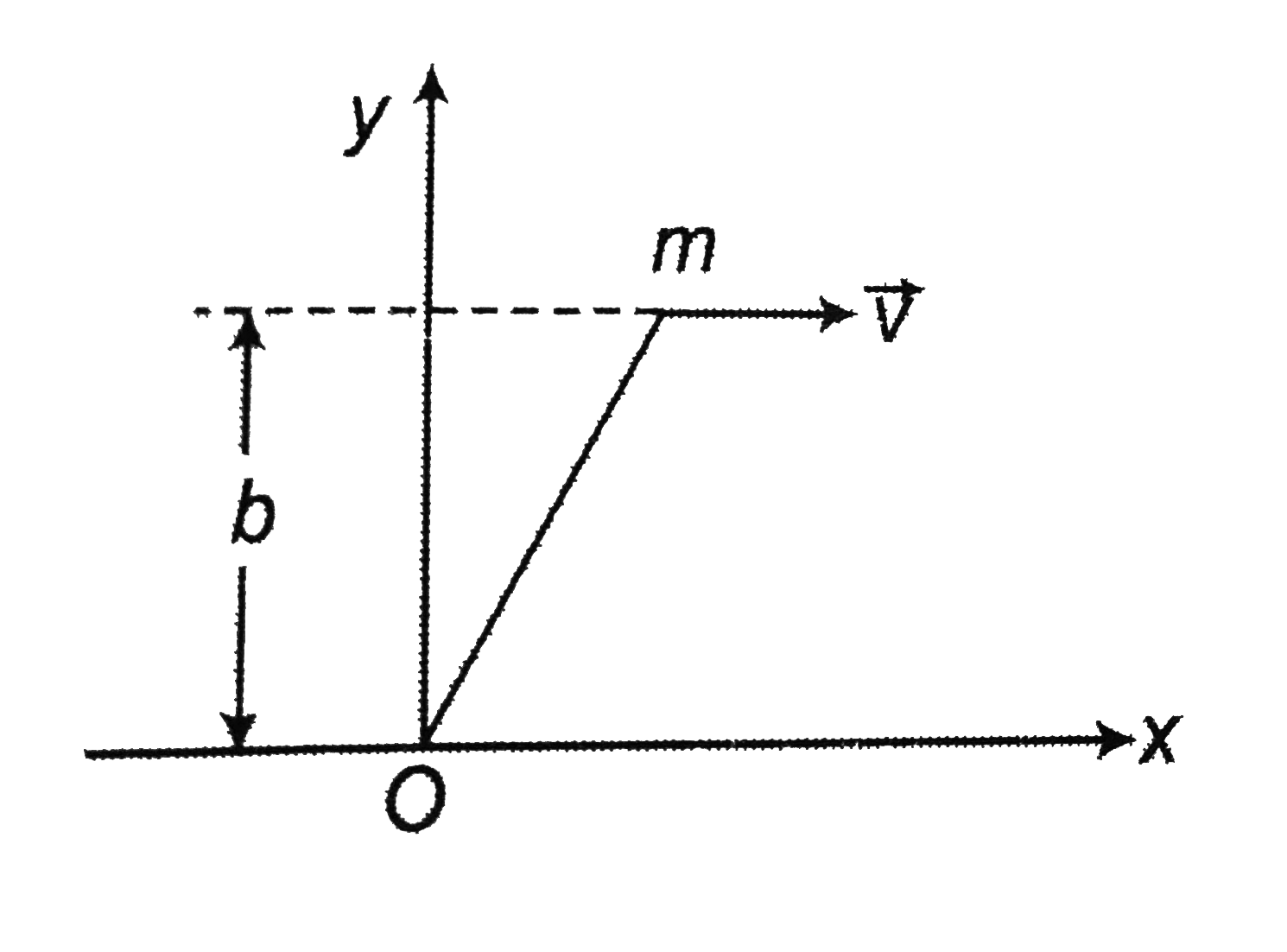
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.
 View Solution
View SolutionA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
View Solution


