A particle of mass is projected with a speed at an angle of projection with horizontal. Find the torque of the weight of the particle about the point of projection after time
In projectile motion,
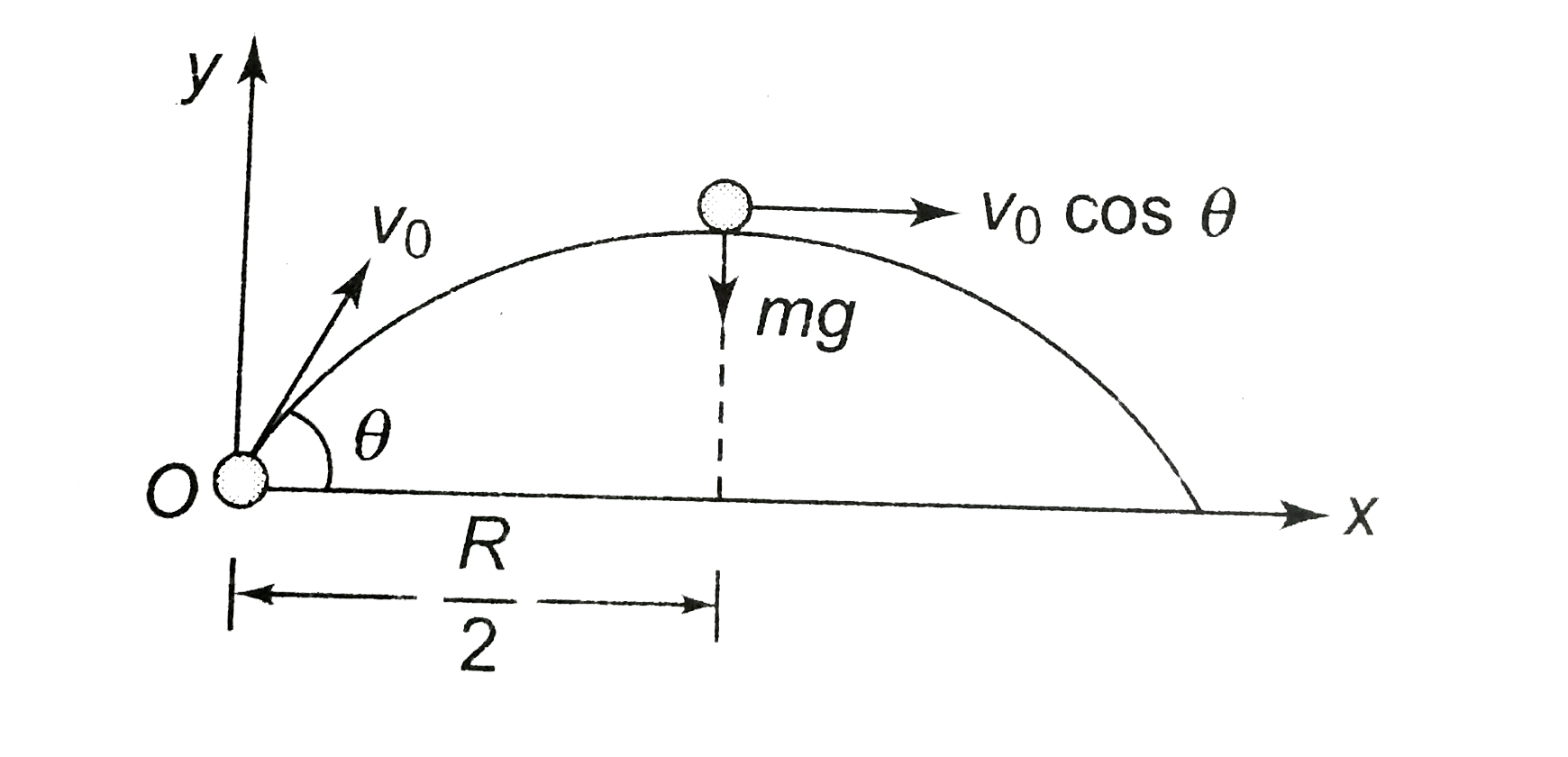
Time of flight
Horizontal range
After time , the particle is at highest point.
Torque of wieght about point of projection
Topper's Solved these Questions
Similar Questions
A particle of mass m is projecte dwilth speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
Knowledge Check
A particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
Amu3sin2θcosθ3gB3mu3sin2θcosθ3gCmu3sin2θcosθ2gD2mu3sinθcos2θ3gA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
AmU2Sin2θ2BmU2Sin2θCmU2Sinθ2D12mU2(Sin2θ)2A particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
AgcosθθvBgvsinθCgvθDgθvsinθ
A particle is projected with a speed v at an angle θ with the horizontal. Find the mean power delivered by gravity during the ascent of the particle.
View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is
View SolutionA particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
View Solution

