A small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
√2gh
√2g(R+h)
√2g(R−h)
None of these
The correct Answer is:C
To solve the problem of determining the speed at which a small ball should be pushed from a height h along a smooth hemispherical bowl of radius R so that it just reaches the top of the opposite end of the bowl, we can use the principle of conservation of mechanical energy.
1. Identify the Initial and Final States:
- Initial State (Point A): The ball is pushed from a height h with an initial speed u.
- Final State (Point B): The ball reaches the top of the hemisphere, where its speed is 0.
2. Write the Energy Conservation Equation:
The total mechanical energy at point A must equal the total mechanical energy at point B, since there are no non-conservative forces (like friction) acting on the ball.
Potential Energy (PE)+Kinetic Energy (KE) at A=PE+KE at B
UA+KA=UB+KB
3. Calculate the Energies:
- At point A:
- Potential Energy UA=mgh (where m is the mass of the ball)
- Kinetic Energy KA=12mu2
- At point B:
- Potential Energy UB=mgR (the height at point B is R)
- Kinetic Energy KB=0 (since the speed at the top is 0)
4. Set Up the Equation:
Substituting the energies into the conservation equation:
mgh+12mu2=mgR+0
5. Simplify the Equation:
We can cancel the mass m from all terms (assuming m≠0):
gh+12u2=gR
6. Rearranging the Equation:
Rearranging gives:
12u2=gR−gh
u2=2g(R−h)
7. Solve for u:
Taking the square root of both sides:
u=√2g(R−h)
Final Answer:
The speed u at which the ball should be pushed is:
u=√2g(R−h)
- Initial State (Point A): The ball is pushed from a height h with an initial speed u.
- Final State (Point B): The ball reaches the top of the hemisphere, where its speed is 0.
The total mechanical energy at point A must equal the total mechanical energy at point B, since there are no non-conservative forces (like friction) acting on the ball.
Potential Energy (PE)+Kinetic Energy (KE) at A=PE+KE at B
UA+KA=UB+KB
- At point A:
- Potential Energy UA=mgh (where m is the mass of the ball)
- Kinetic Energy KA=12mu2
- At point B:
- Potential Energy UB=mgR (the height at point B is R)
- Kinetic Energy KB=0 (since the speed at the top is 0)
Substituting the energies into the conservation equation:
mgh+12mu2=mgR+0
We can cancel the mass m from all terms (assuming m≠0):
gh+12u2=gR
Rearranging gives:
12u2=gR−gh
u2=2g(R−h)
Taking the square root of both sides:
u=√2g(R−h)
The speed u at which the ball should be pushed is:
u=√2g(R−h)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
View SolutionA ball of mass m is released from rest from a height H along a smooth, light and fixed tube having a semicircular portion so that the ball just reaches the top of the semicircle.
a. Find the radius of the semi-circle.
b. Find the maximum force imparted by the ball on the ground.

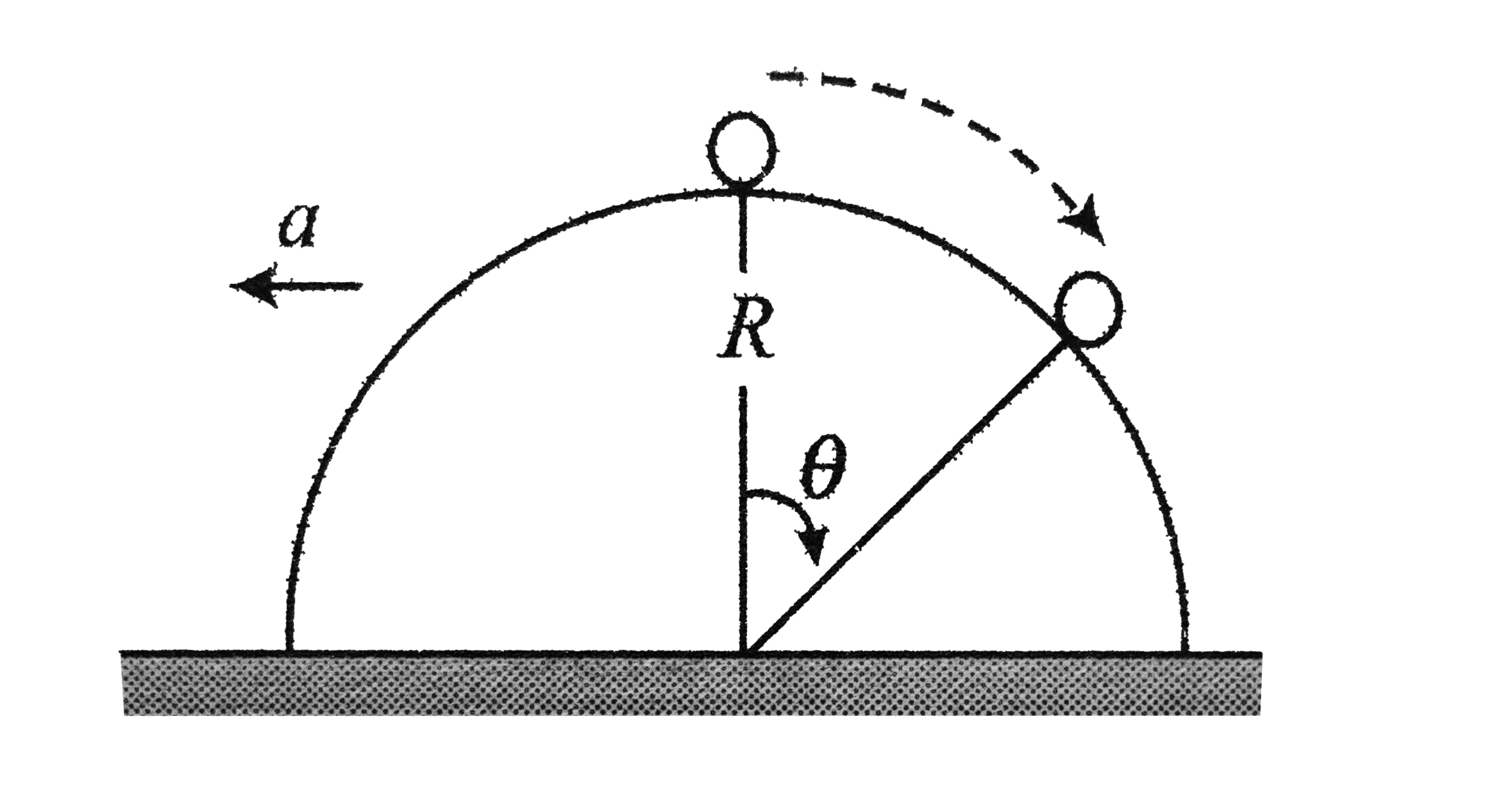
View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

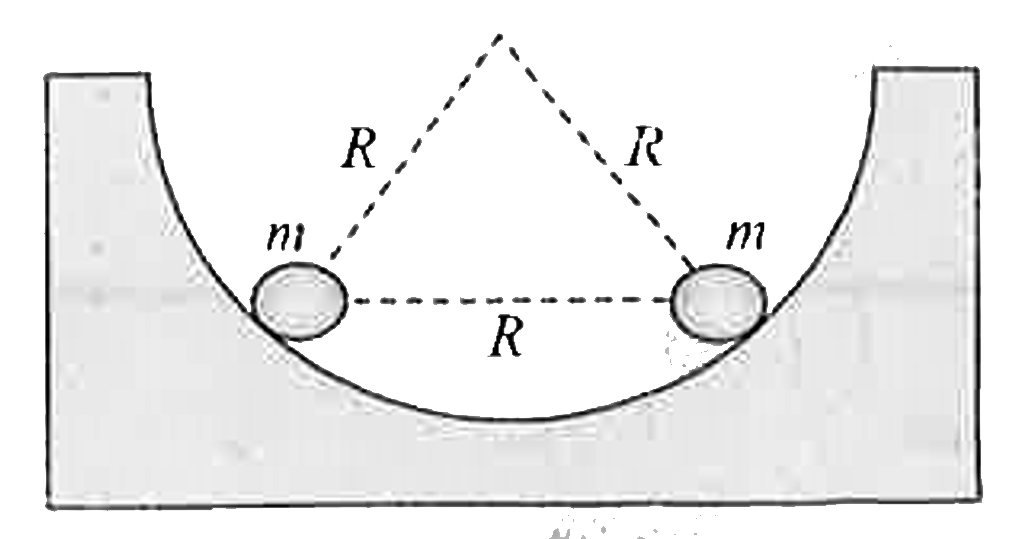
View SolutionTwo identical small balls each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, nonconductive walls, the bead move, and at equilibrium the line joining the balls is horizontal and the distance between them is R (see figure). Neglect any induced charge on the hemispherical bowl. Then the charge on each bead is : (here K=14πε0)
View SolutionA small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
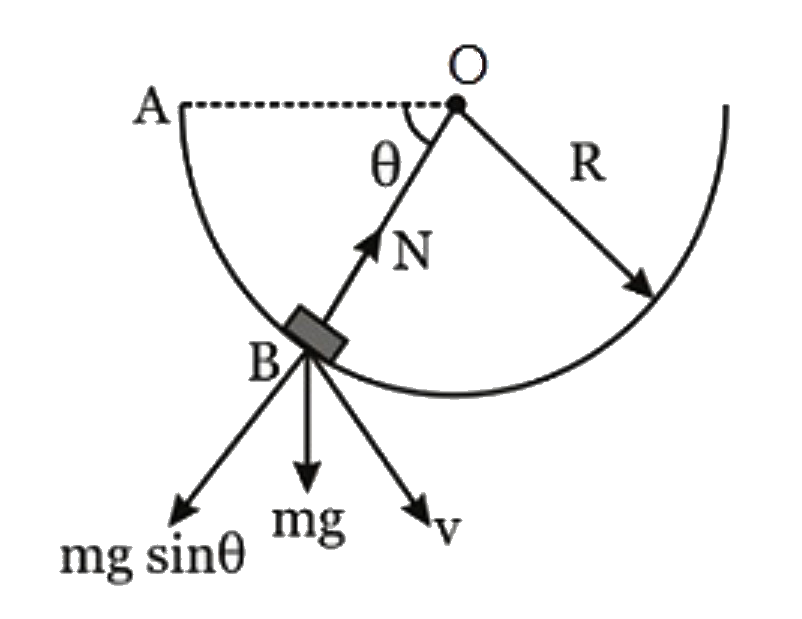
View SolutionA small block of mass m is released from rest from point A inside a smooth hemispher bowl of radius R, which is fixed on ground such that OA is horizontal. The ratio (x) of magnitude of centripetal force and normal reaction on the block at any point B varies with θ as :
View SolutionA small block of mass m is released from rest from point A inside a smooth hemisphere bowl of radius R, which is fixed on group such that OA is horizontal. The ratio (x) of magnitude of centripetal force and normal reaction on the block at any point B varies with θ as :

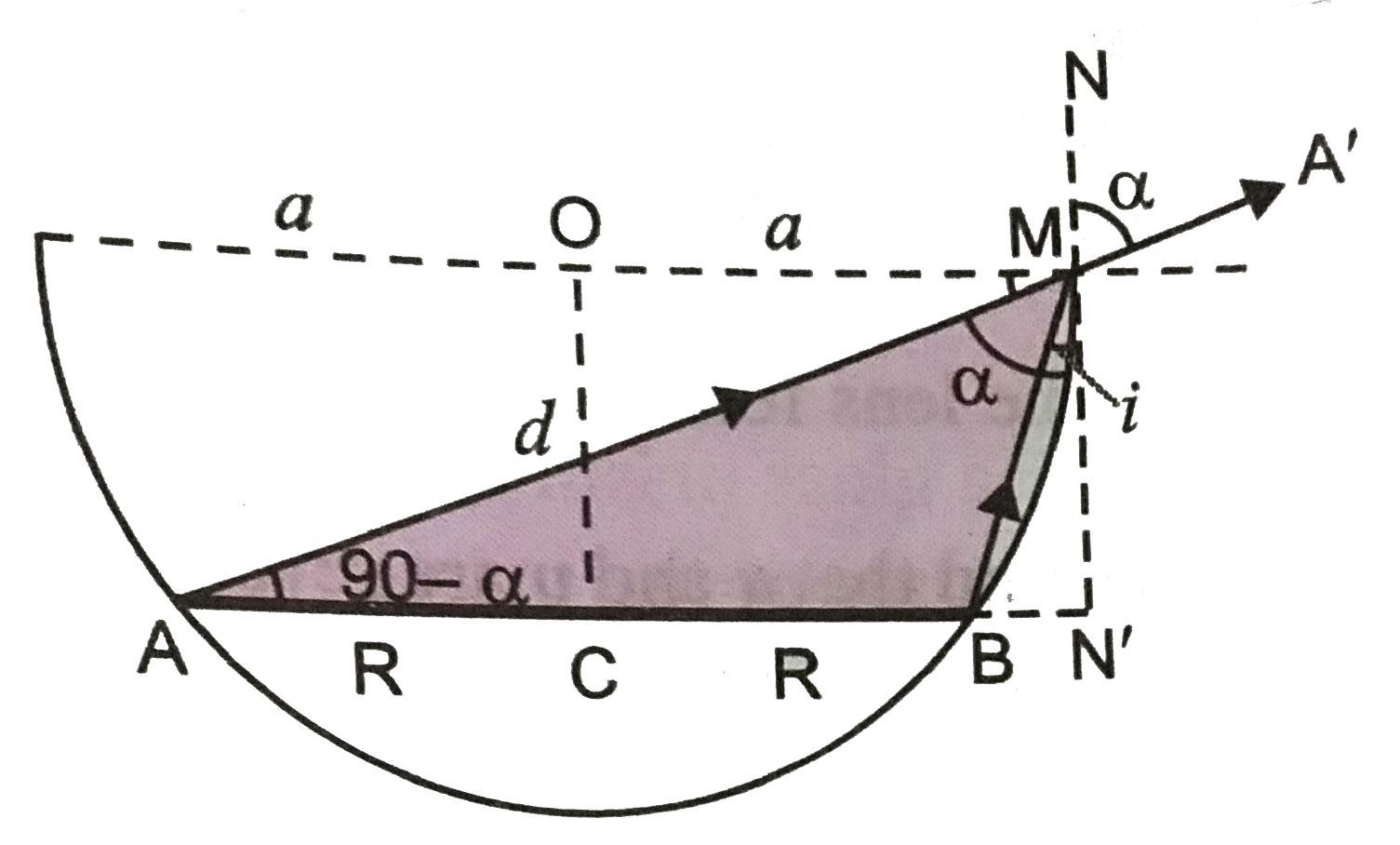
View SolutionA circuilar disc of radius 'R' is placed co-axially and horizontally inside and opaque hemispherical bowl of radius 'a', Fig. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the dise becomes just visible. How far below the top of the bowl is the disc placed ?
 .
.
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the surface of hemisphere?

View Solution

