A constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?

a. The direction of the frictional force will be in backwark direction of motion of the wheel.
10−f=ma
Substituting m=10kg and a=0.60m/s2 in the above equation, we get
Fr=4N
b. Equation of motion for rotation of wheel
fr×R=Iα
which gives
I=fr×Rα4×0.30(0.600.30)
or I=0.6kgm2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A horizontal force F=14N acts at the centre of mass of a sphere of mass m=1kg. If the sphere rolls without sliding, find the frictional force (in N)

View Solution
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is

View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is

View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is

View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
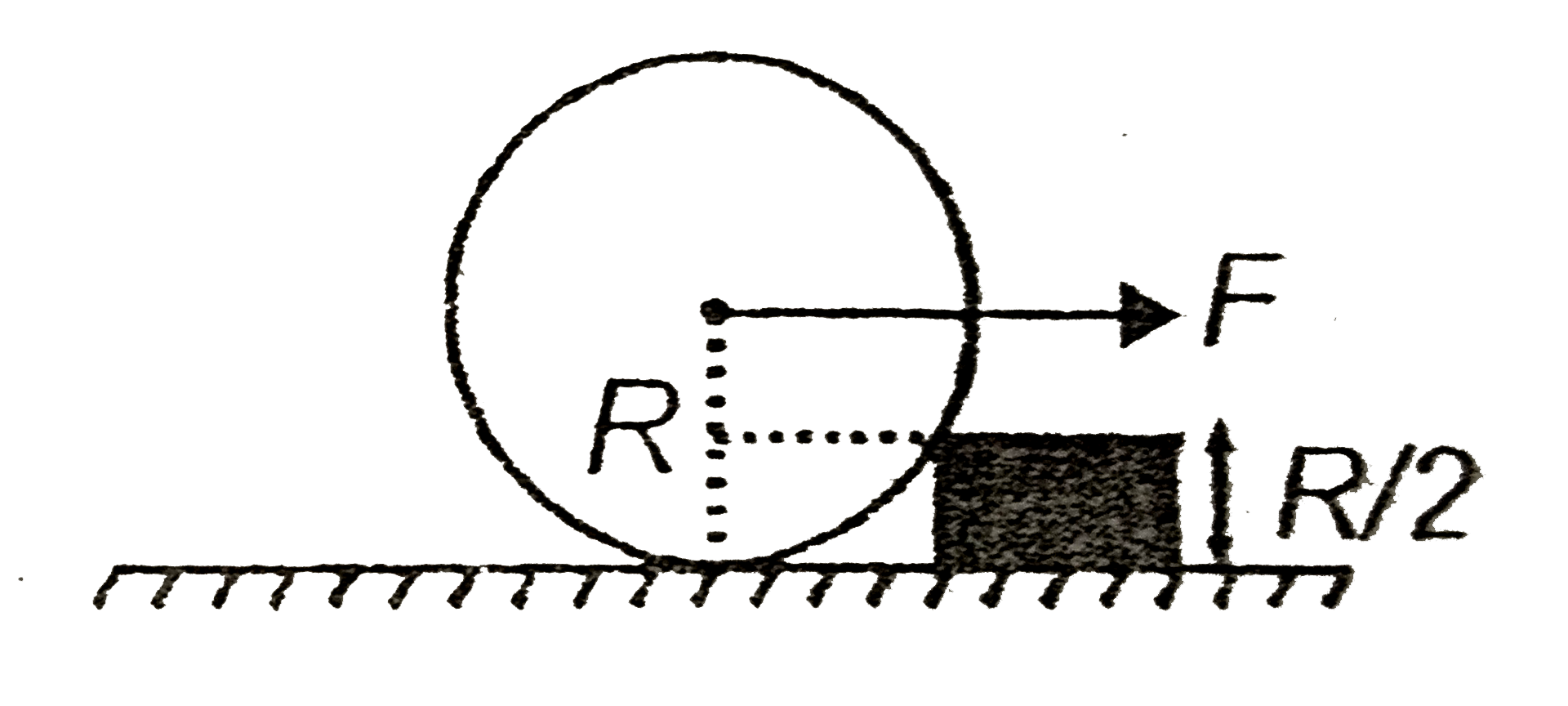
View Solution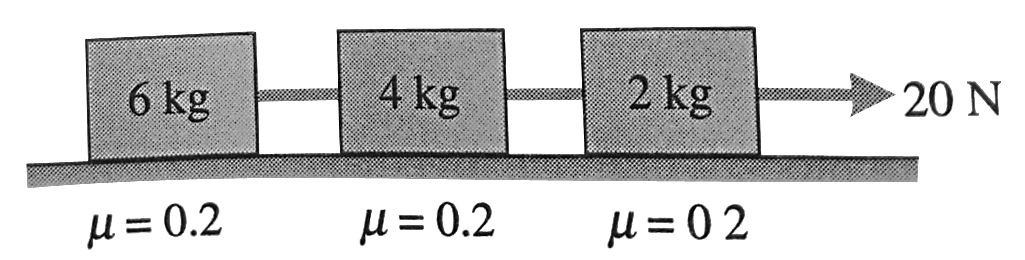
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View Solution

