A uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
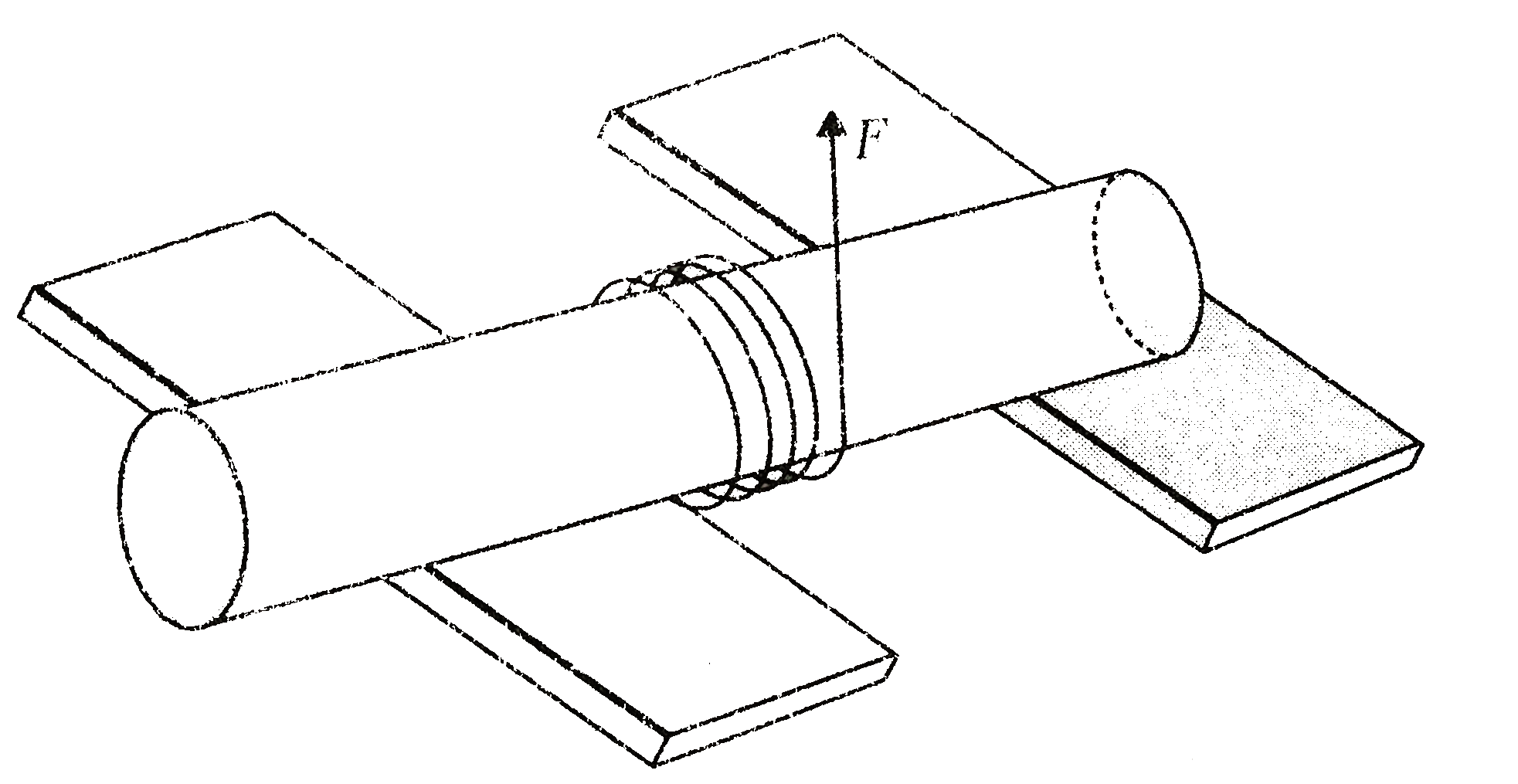
As the force F is applied the cylinder tends to rotate along anticlockwise direction with the point of contact C tending to move to the right. Hence, friction acts along the left (as shown in figure) If α is the angular acceleration of the cylinder then from τ=Iα we have
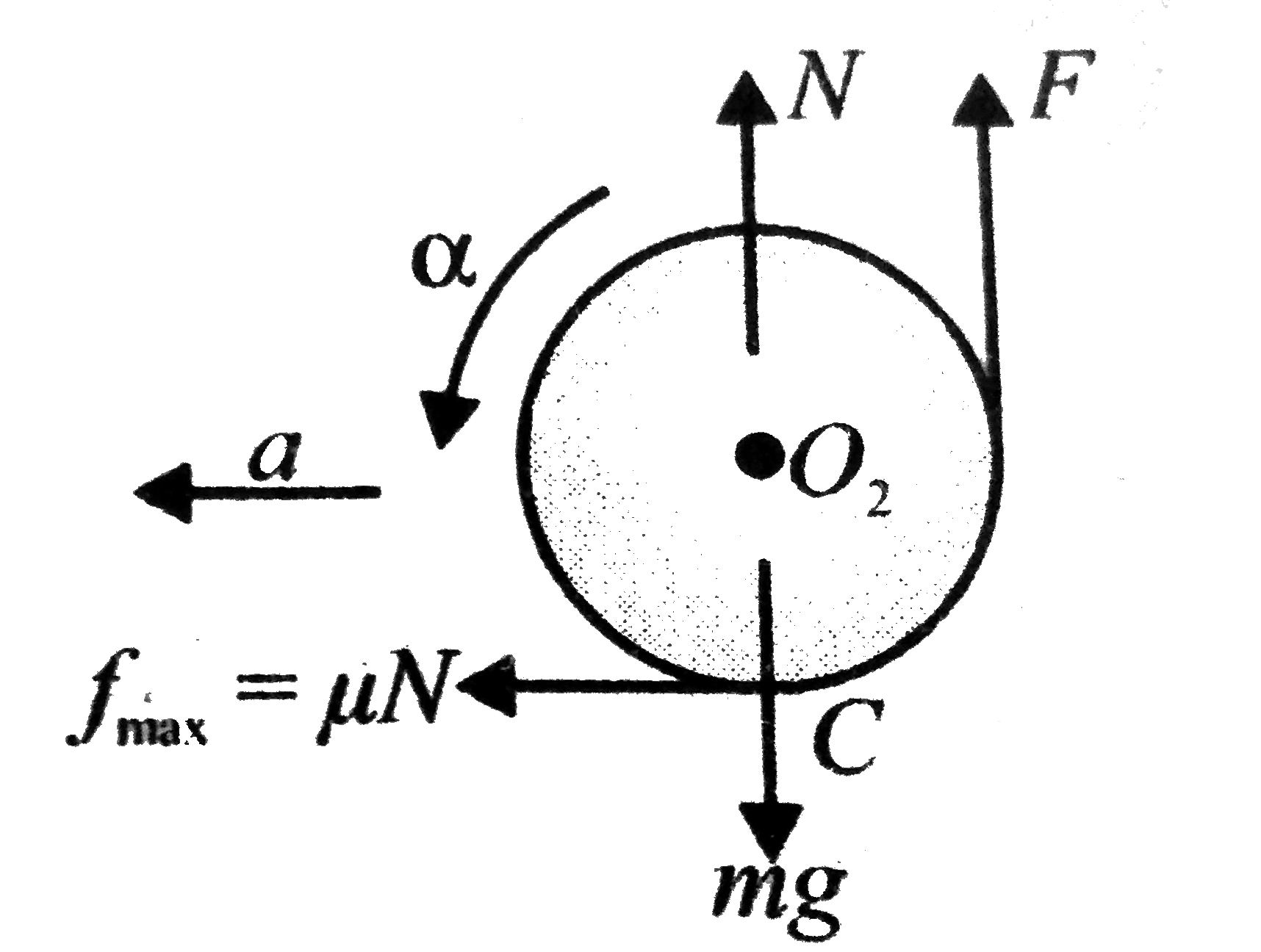
r(F−r)=(mr2/2)α...i
If a is the linear acceleratioin of the cylinder's CM, then from F=ma we have
f=ma........ii
For pure rolling,
a=αr............iii
Dividing Eq i by eqn ii we get
(F−f)f=rα2a=12
⇒F=(3f2)⇒Fmax=(32)fmax
[fmax=μN⇒μ(mg−F)]
⇒Fmax=3μ2[m≡LFmax]=3μmg2+3μ
from eq ii
a=fm
⇒amax=fmaxm=23mFmax=23m(3μmg2+3μ)=2μg2+3μ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
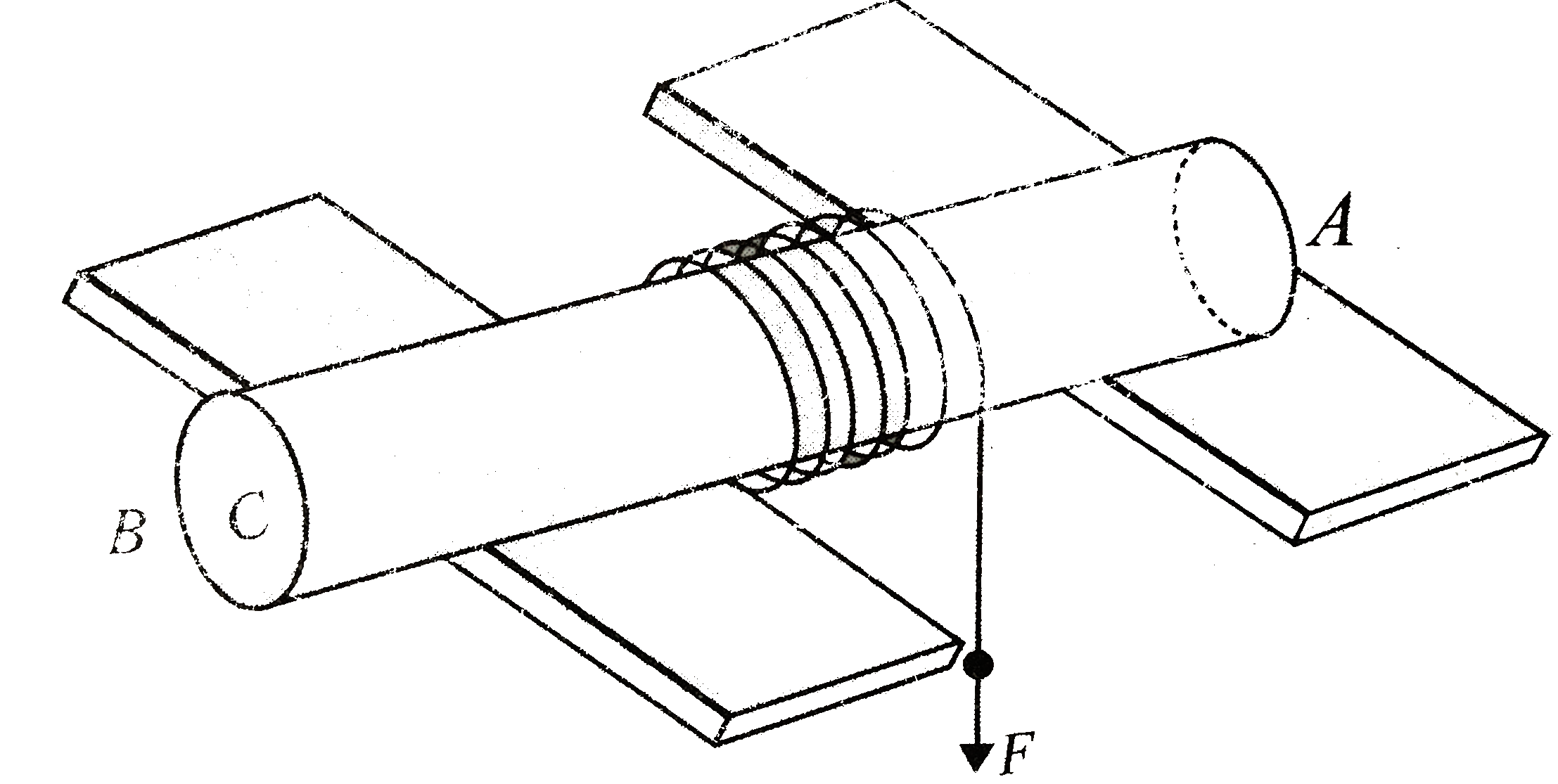
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?View Solution
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?View Solution
Knowledge Check
- Question 1 - Select One
A rope is wound round a hollow cylinder of mass 3kgandradius40cm. If the rope is pulled with a force of 30N, what is the angualr acceleration of the cylinder ?
A15rads−2B20rads−2C25rads−2D30rads−2

A cylinder of radius R is to roll without slipping between two planks as shown in the figure. ThenView SolutionA cylinder of weight W and radius R is to be raised onto a horizontal step of height h as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force F. Assuming the cylinder does not slip on the step, find the minimum force F necessary to raise the cylinder.
 View Solution
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionThe figure shows a spool placed at rest on a horizontal rough surface. A tightly wound string on the inner cylinder is pulled horizontally with a force F. identify the correct alternative related to the friction f acting on the spool
 View Solution
View SolutionA man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
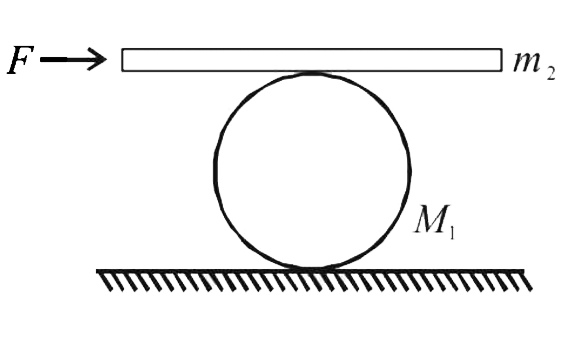
(b) the magnitudes and direction of frictional force at contact points.View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
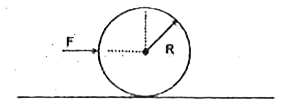 View Solution
View Solution
