A charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
14πε0(2R+r)(R2+r2)Q
14πε0(R+r)(R2+r2)Q
14πε0(R+r)2(R2+r2)Q
14πε0(R+2r)Q2(R2+r2)
The correct Answer is:B
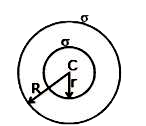
Q1=σ.4πr2
Q2=σ.4πR2
Q=4πσ(R2+r2)
⇒σ=Q4π(R2+r2)
ve=KQr+KQ2R
==Kσ4πr2r=Kσ4πR2R=Kσ4π(r+R)
4πKQ4π(R2+r2)(r+Q)=KQ(r+Q)(R2+r2)
Related Playlists
Similar Questions
A charge .q. is distrubuted over two concertric hollow conducting sphere of radii r and R (<r) such that their surface charge densite are equal. The potential at their common centre is
View SolutionA charge Q is distributed over three concentric spherical shells of radii a, b, c (a< b < c) such that their surface charge densities are equal to one another.
The total potential at a point at distance r from their common centre, where r<a, would be :View SolutionTwo concentric spheres of radii R and r have similar charges with equal surface charge densities (σ). The electric potential at their common centre is
View SolutionTwo connectric spheres of radii R and r have similar charges with equal surface charge densities (sigam). The electric potential at their common centre is
View SolutionA charge Q has been divided on two concentirc conducting spheres of radii R1andR2(R1>R2) such that the surface charge densities on both the sphere is same. Find the potential at their common center.
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionTwo concentric spheres kept in air have radii R and r. They have similar charge and equal surface charge density σ. The electrical potential at their common centre is (where, ε0= permittivity of free space)
View SolutionConcentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View Solution


