A ray incident at an angle of incidence 60∘ enters a glass sphere of μ=√3 and it is reflected and refracted at the farther surface of the sphere. The angle between reflacted and refracted rays at this surface is
To solve the problem step by step, we will use Snell's law and some geometric properties of angles.
Step 1: Identify the given values
- Angle of incidence (i) = 60°
- Refractive index of glass (μ) = √3
- Refractive index of air (n) = 1
Step 2: Apply Snell's Law at the first surface (point A)
Using Snell's law:
n1sin(i)=n2sin(r)
Where:
- n1=1 (air)
- n2=√3 (glass)
- i=60°
- r is the angle of refraction at point A.
Substituting the values:
1⋅sin(60°)=√3⋅sin(r)
sin(60°)=√32
So,
√32=√3⋅sin(r)
Step 3: Solve for sin(r)
Dividing both sides by √3:
sin(r)=12
Thus,
r=30°
Step 4: Determine the angle at the second surface (point B)
Since the angle of incidence and angle of refraction at point A are equal (due to symmetry in the isosceles triangle formed), the angle at point B will also be 30°.
Step 5: Apply Snell's Law at the second surface (point B)
Using Snell's law again:
n2sin(r)=n1sin(e)
Where:
- n2=√3
- n1=1
- r=30°
- e is the angle of refraction at point B.
Substituting the values:
√3⋅sin(30°)=1⋅sin(e)
Since sin(30°)=12:
√3⋅12=sin(e)
Thus,
sin(e)=√32
So,
e=60°
Step 6: Calculate the angle between the reflected and refracted rays
The angle of reflection (α) at point B is equal to the angle of incidence (r) at that point, which is also 30°.
Now, we can find the angle between the reflected ray and the refracted ray:
- Reflected ray makes an angle of 30° with the normal.
- Refracted ray makes an angle of 60° with the normal.
The angle between the reflected and refracted rays is:
Angle=α+e=30°+60°=90°
Final Answer
The angle between the reflected and refracted rays at the farther surface of the sphere is 90°.
---
- Angle of incidence (i) = 60°
- Refractive index of glass (μ) = √3
- Refractive index of air (n) = 1
Using Snell's law:
n1sin(i)=n2sin(r)
Where:
- n1=1 (air)
- n2=√3 (glass)
- i=60°
- r is the angle of refraction at point A.
1⋅sin(60°)=√3⋅sin(r)
sin(60°)=√32
So,
√32=√3⋅sin(r)
Dividing both sides by √3:
sin(r)=12
Thus,
r=30°
Since the angle of incidence and angle of refraction at point A are equal (due to symmetry in the isosceles triangle formed), the angle at point B will also be 30°.
Using Snell's law again:
n2sin(r)=n1sin(e)
Where:
- n2=√3
- n1=1
- r=30°
- e is the angle of refraction at point B.
√3⋅sin(30°)=1⋅sin(e)
Since sin(30°)=12:
√3⋅12=sin(e)
Thus,
sin(e)=√32
So,
e=60°
The angle of reflection (α) at point B is equal to the angle of incidence (r) at that point, which is also 30°.
- Reflected ray makes an angle of 30° with the normal.
- Refracted ray makes an angle of 60° with the normal.
Angle=α+e=30°+60°=90°
The angle between the reflected and refracted rays at the farther surface of the sphere is 90°.
Topper's Solved these Questions
Similar Questions
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View Solution
Knowledge Check
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
A50∘B60∘C90∘D40∘A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
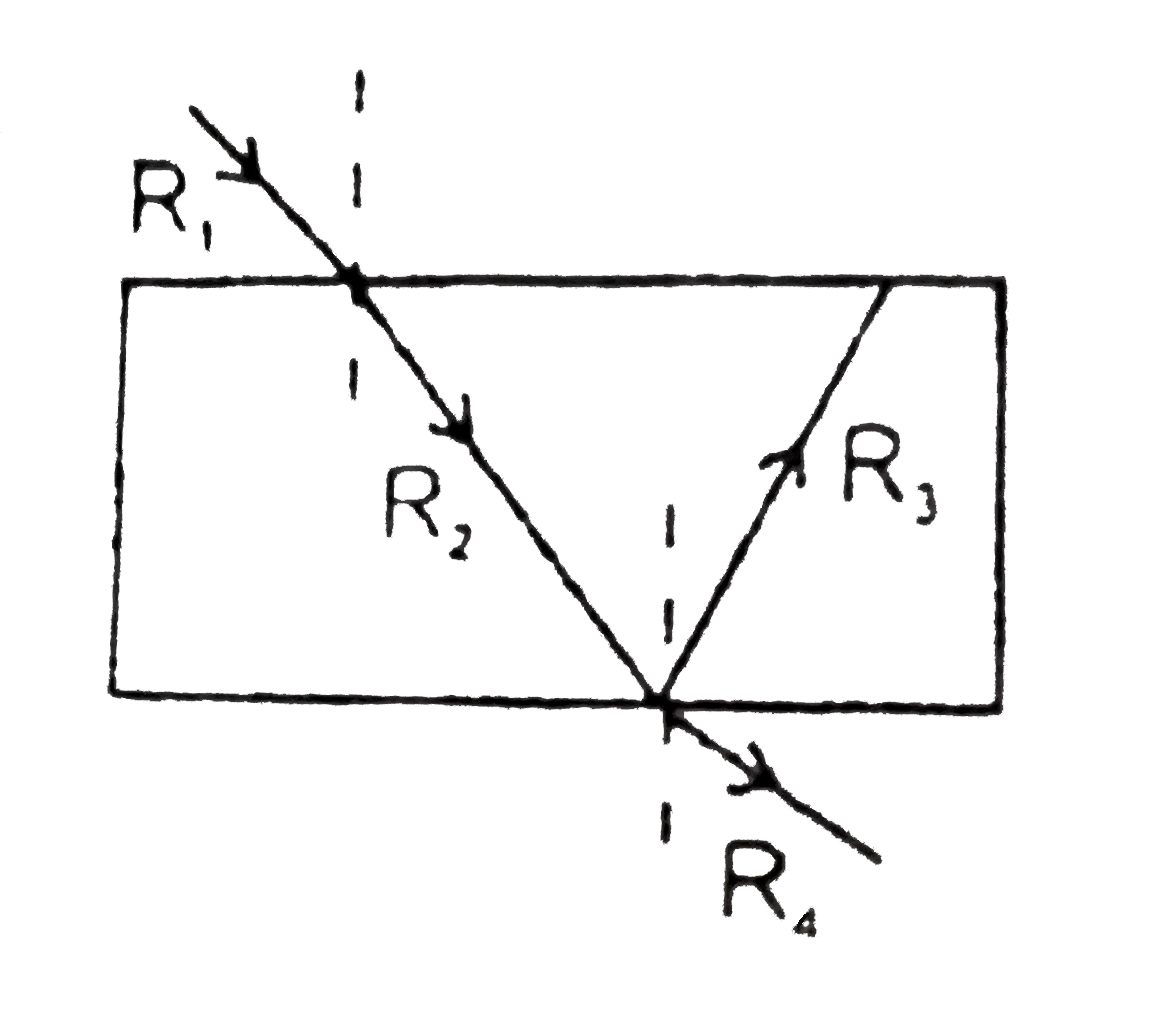
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :

View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution