If r is the radius of spherical balloon at time t and the surface area

If the radius of a spherical balloon increases by 0.1% then its volume increases approximately by
A $0.2 %$
B $0.3 %$
C $0.4 %$
D $0.05 %$
The radius of spherical bubble is changing with time. The rate of change of its volume is given by :
A $4 π r^{2} \frac{d r}{d t}$
B $\frac{4}{3} π r^{2}$
C $\frac{8}{3} π r^{2}$
D $\frac{8}{3} π r \frac{d r}{d t}$
A conducting bolloon of the radius a is charged to potential $V_{0}$ and held at a large height above the earth ensures that charge distribution on the surface of the balloon remains unaffected by the presence of the earth. It is connected to the earth through a resistance R and a value in the balloon is opened . The gas inside the balloon escapes from value and the size of the balloon decreases. The rate of decrease in radius of the balloon is controlled in such a manner that potential of the balloon remains constant. Assume the electric permittivity of the surrounding air equals to that of free space $(ε_{0})$ and charge cannot leak to the surrounding air.

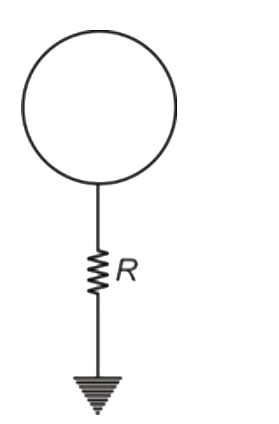
The rate at which radius r of the balloon changes with time is best represented by the equation
A $\frac{d r}{d t} = \frac{1}{4 π ε_{0} R}$
B $\frac{d r}{d t} = - \frac{1}{4 π ε_{0} R}$
C $\frac{d r}{d t} = \frac{1}{4 π ε_{0} a R}$
D $\frac{d r}{d t} = - \frac{r}{4 π ε_{0} a R}$

If r is the radius of spherical balloon at time t and the surface area of balloon changes at a constant rate K, then . . ..