The area of the region enclosed between pair of the lines xy=0 and the lines xy+5x-4y-20=0, is

A

20 square units

B

$\frac{4}{5}$ square units

C

10 square units

D

6 square units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Gvien pair of lines
$x y + 5 x - 4 y - 20 = 0$
$\Rightarrow x (y + 5) - 4 (y + 5) = 0$
$\Rightarrow (y + 5) (x - 4) = 0$
$\Rightarrow (y + 5) (x - 4) = 0$
$\Rightarrow x = 4, y = - 5$
and also, xy=0 $\Rightarrow x = 0, y = 0$
Now, draw the graph of the pairs of line

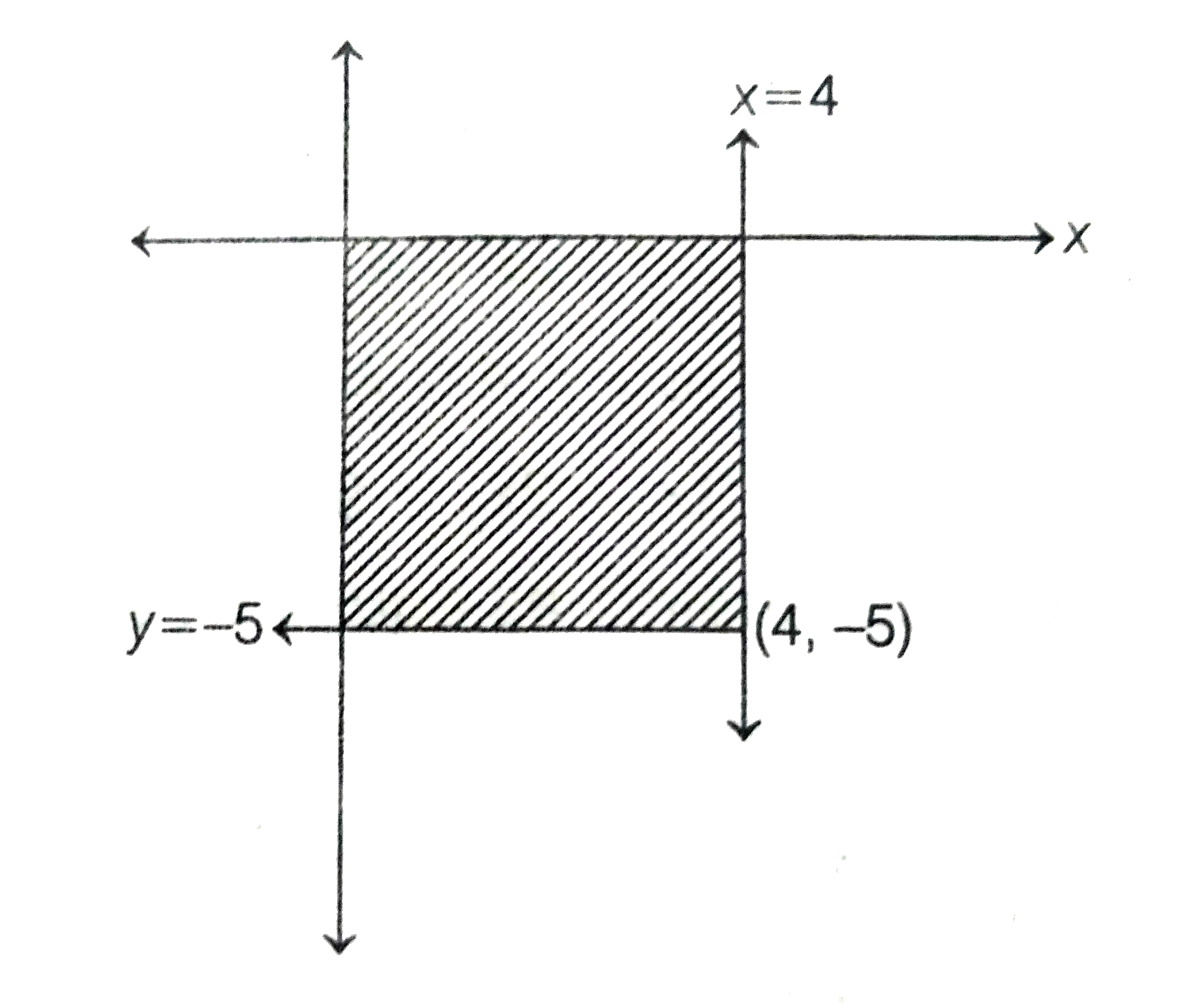
$∴$ Required area of bounded region $= 4 \times 5 = 20$ sq. units.

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Angle between the pair of lines $x y = 0$ is
A $30^{\circ}$
B $45^{\circ}$
C $90^{\circ}$
D $60^{\circ}$
Orthocentre of the triangle formed by the pair of lines $x y = 0$ and the lines $2 x + 3 y + 4 = 0$ is
A $(2, 3)$
B $(3, 2)$
C $(0, 0)$
D $(4, - 4)$
What is the area of the region bounded by the lines $y = x . y = 0$ and x=4?
A4 sq. units
B8 sq. units
C12 sq. units
D16 sq. units

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-SOLVED PAPER 2019-MCQS

Home
Ask Doubt
Profile